Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

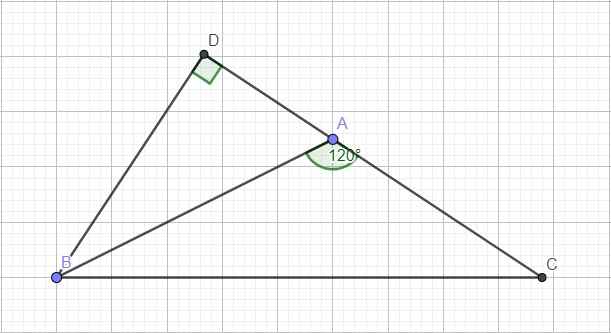
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)

Câu 2:
Từ B, kẻ đường thẳng vuông góc với BC cắt AC tại M.
Từ giả thiết, ta có:
\(\cdot\) AH // BM (do cùng _I_ BC)
\(\cdot\) H là trung điểm của BC (\(\Delta ABC\) cân tại A có AH là đường cao)
Suy ra AH là đường trung bình của \(\Delta BMC\)
\(\Rightarrow BM=2AH\)
Xét \(\Delta BMC\) vuông tại B có BK là đường cao
\(\Rightarrow\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{BM^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\) (đpcm)
Câu 1:
Xét \(\Delta ABC\) vuông tại A có AH là đường cao
\(\Rightarrow AB^2=BH\times BC\)
Xét \(\Delta HBA\) vuông tại H có HE là đường cao
\(\Rightarrow BH^2=BE\times AB\)
\(\Rightarrow BE^2=\dfrac{BH^4}{AB^2}=\dfrac{BH^4}{BH\times BC}=\dfrac{BH^3}{BC}\)
Chứng minh tương tự, ta có: \(CF^2=\dfrac{CH^3}{BC}\)
Suy ra \(\sqrt[3]{BE^2}+\sqrt[3]{CF^2}=\dfrac{BH}{\sqrt[3]{BC}}+\dfrac{CH}{\sqrt[3]{BC}}=\dfrac{BH+CH}{\sqrt[3]{a}}=\dfrac{a}{\sqrt[3]{a}}=\left(\sqrt[3]{a}\right)^2\)
bn tự vẽ hình nha !
đặt CH=b'
Xét tam giác BHC vuông tại H có:
a2= BH2 + b'2(Đlí pi-ta-go)(1)
Xét tam giác ABH vuông tại H có:
=> BH2 = AB2-AH2=c2 - c'2
Từ (1) => a2= c2-c'2+b'2
=c2-c'2+(b-c')2 ( Vì b' +c'=b)
=c2+b2-2bc' (ĐPCM)