Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy F là điểm đối xứng với B qua AM, gọi O là giao điểm của BF với AM
\(\Delta\)AOB vuông tại O có ^MAB = 300 (gt) nên ^ABO = 600
Lại có: AF = AB (theo tính chất đối xứng) nên \(\Delta\)AFB đều => ^AFB = 600
\(\Delta\)AFB đều có AO là đường cao nên cũng là trung tuyến => FO = OB
Có M là trung điểm của BC, O là trung điểm của FB nên OM là đường trung bình của \(\Delta\)BFC
=> OM // CF mà OM\(\perp\)FB nên BF\(\perp\)FC => \(\Delta\)BFC vuông tại F hay ^BFC = 900
Ta có: ^CFA = ^BFC + ^BFA = 900 + 600 = 1500
\(\Delta\)AFB đều có AO là đường cao nên cũng là phân giác => ^OAF = 300 => ^FAC = 150
Suy ra ^FCA = 150 hay \(\Delta\)CFA cân tại F => CF = AF
Mà AF = FB nên BF = FC do đó \(\Delta\)BFC vuông cân tại F => ^FBC = 450
=> ^ABC = ^CBF + ^FBA = 450 + 600 = 1050
Vậy ^BCA = 1800 - 1050 - (150 + 300) = 300

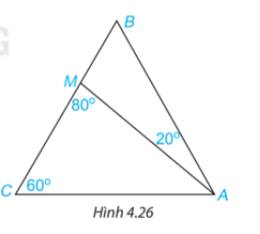
Ta có:
\(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}\)
Áp dụng định lí tổng ba góc trong một tam giác:
+) Trong tam giác AMB có:
\(\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}\)
+) Trong tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}\)

a) Xét tam giác ABM và tam giác ECM có :
AM = ME
\(\widehat{AMB}=\widehat{CME}\left(đđ\right)\)
BM = MC
\(\Rightarrow\) tam giác ABM = tam giác ECM ( c-g-c ) (đpcm)
b) Do tam giác ABM = tam giác ECM
\(\Rightarrow AB=CE\) (1)
Mà tam giác ABC vuông tại B
\(\Rightarrow AC>AB\) ( do cạnh AC là cạnh huyền ) (2)
Từ (1) và (2) \(\Rightarrow AC>CE\left(đpcm\right)\)
c) Xét tam giác ACE có : \(AC>CE\)
\(\Rightarrow\widehat{MAC}< \widehat{CEA}\left(3\right)\)
Mà tam giác ABM = tam giác ECM ( câu a )
\(\Rightarrow\widehat{BAM}=\widehat{CEA}\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\widehat{BAM}>\widehat{MAC}\left(đpcm\right)\)