Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải một ý thôi
Ta có: \(\widehat{ACK}=\widehat{A}+\widehat{AEC}=\widehat{A}+90^o\)( tính chất góc ngoài)
\(\widehat{ABH}=\widehat{A}+\widehat{ADB}=\widehat{A}+90^o\)( tính chất góc ngoài)
\(\Rightarrow\widehat{ACK}=\widehat{ABH}\)
Xét tam giác ABH và tam giác KCA có:
\(\Rightarrow\Delta ABH=\Delta KCA\left(c-g-c\right)\hept{\begin{cases}BH=CA\left(gt\right)\\\widehat{ABH}=\widehat{KCA}\left(cmt\right)\\AB=CK\left(gt\right)\end{cases}}\)
\(\Rightarrow AH=AK\)(cạnh tương ứng)
=> đpcm

Ta có: ^ACK=^A+^AEC=^A+90o( tính chất góc ngoài)
^ABH=^A+^ADB=^A+90o( tính chất góc ngoài)
⇒^ACK=^ABH
Xét tam giác ABH và tam giác KCA có:
⇒ΔABH=ΔKCA(c−g−c){
| BH=CA(gt) |
| ^ABH=^KCA(cmt) |
| AB=CK(gt) |
⇒AH=AK(cạnh tương ứng)
=> đpcm

Có \(\widehat{ABD}+\widehat{A}=\widehat{A}+\widehat{ACE}=90^0\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\)
\(\Rightarrow180^0-\widehat{ABD}=180^0-\widehat{ACE}\)
\(\Leftrightarrow\widehat{ABH}=\widehat{ACK}\)
Xét tam giác ABH và tam giác ACK có:
\(AB=CK\)
\(\widehat{ABH}=\widehat{ACK}\)
\(HB=AC\)
nên tam giác ABH= tam giác KCA (c.g.c)
\(\Rightarrow AH=AK\)
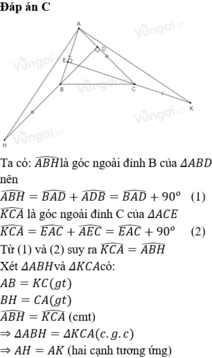
a) Ta có:
\(\widehat{ACK}=\widehat{A}+\widehat{AEC}\) ( tính chất góc ngoài của tam giác ).
=> \(\widehat{ACK}=\widehat{A}+90^0\) (1).
\(\widehat{ABH}=\widehat{A}+\widehat{ADB}\) ( tính chất góc ngoài của tam giác ).
=> \(\widehat{ABH}=\widehat{A}+90^0\) (2).
Từ (1) và (2) => \(\widehat{ABH}=\widehat{ACK}.\)
Hay \(\widehat{ABD}=\widehat{ACE}.\)
b) Xét 2 \(\Delta\) \(ABH\) và \(KCA\) có:
\(BH=CA\left(gt\right)\)
\(\widehat{ABH}=\widehat{ACK}\left(cmt\right)\)
\(AB=CK\left(gt\right)\)
=> \(\Delta ABH=\Delta KCA\left(c-g-c\right)\)
=> \(AH=AK\) (2 cạnh tương ứng) (đpcm).
Chúc bạn học tốt!