Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đặt vn = un – 1.
Lấy số dương d > 0 bé tùy ý
⇒ luôn tồn tại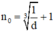 
thỏa mãn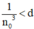 
⇒ 
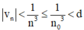với mọi n ≥ n0.
⇒ Theo định nghĩa ta có:
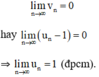
Chọn D
Ta có u n là cấp số nhân công bội bằng 2.
Ta có
2 4 u 1 + 1 + 2 3 - 2 u 2 = 2 4 u 1 + 1 + 2 3 - 4 u 1 ≥ 2 2 4 u 1 + 1 . 2 3 - 4 u 1 = 8
Mặt khác
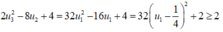
Suy ra
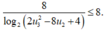
Vậy 2 4 u 1 + 1 + 2 3 - 2 u 2 = 8 log 2 ( 2 u 3 2 - 8 u 2 + 4 )
suy ra giá trị nhỏ nhất của n cần tìm là 2021
l i m v n = 0 ⇒ | v n | có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi (1)
Vì | u n | ≤ v n v à v n ≤ | v n | với mọi n, nên | u n | ≤ | v n | với mọi n. (2)
Từ (1) và (2) suy ra | u n | cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi, nghĩa là l i m u n = 0
Lấy số dương ε bé tùy ý bất kì:
⇒ có một số n0 thỏa mãn: |vn| < ε kể từ n = n0.
⇒ |un – 2| < vn < |vn| < ε kể từ n = n0 trở đi
⇒ lim (un – 2) = 0
⇒ lim un = 2.
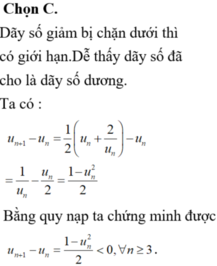
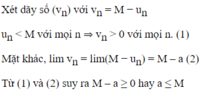
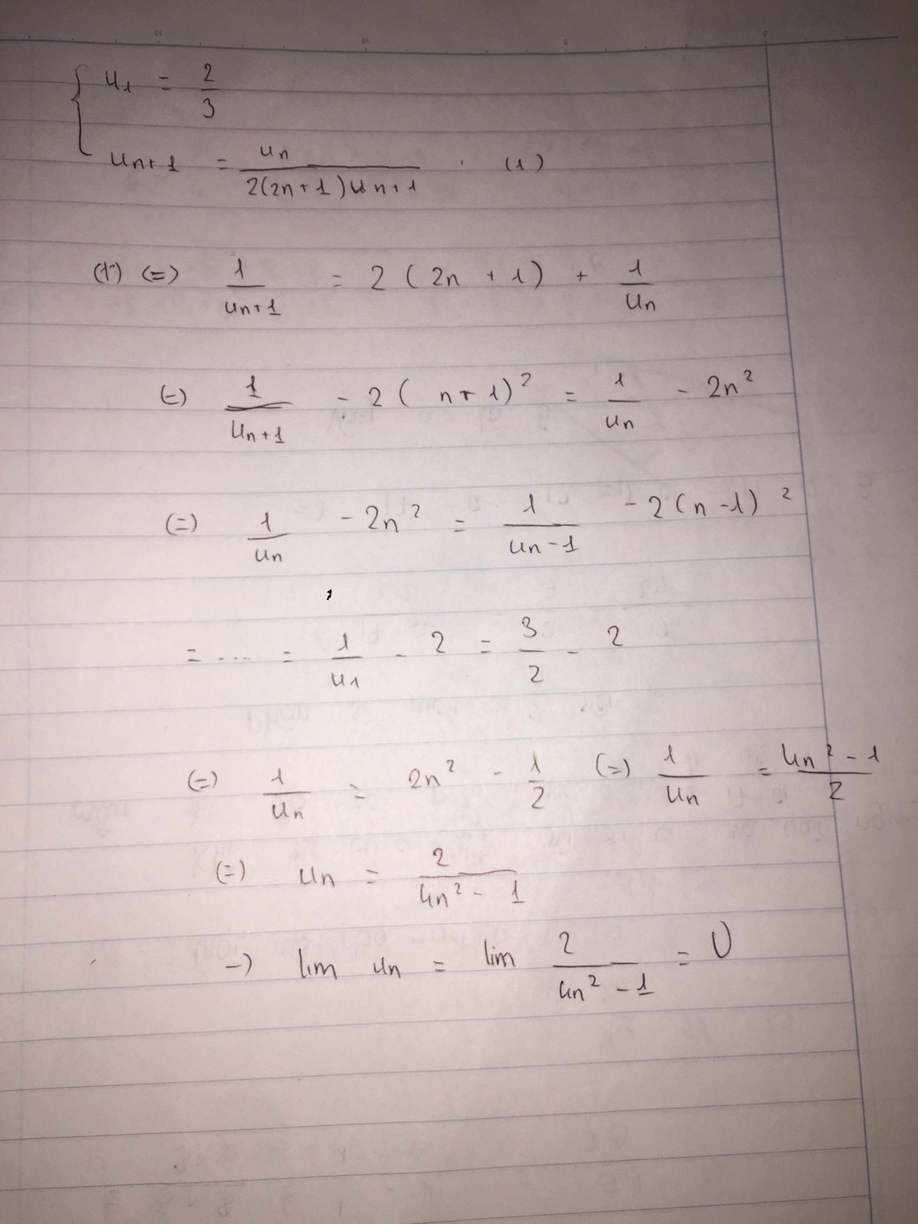
\(\lim\left(u_n-2\right)=0\) ;\(\forall n\Rightarrow\lim\left(u_n\right)=2\)
\(\Rightarrow\lim\left(u_n^2+2u_n-1\right)=2^2+2.2-1=7\)