Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
góc ABH=góc EBH
=>ΔBHA=ΔBHE
b: Xét ΔBAK và ΔBEK có
BA=BE
góc ABK=góc EBK
BK chung
=>ΔBAK=ΔBEK
=>góc BEK=90 độ
=>EK vuông góc BC
c: AK=KE
KE<KC
=>AK<KC

b: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
góc ABH=góc EBH
=>ΔBHA=ΔBHE
c: ΔBHA=ΔBHE
=>BA=BE
Xét ΔBAK và ΔBEK có
BA=BK
góc ABK=góc EBK
BK chung
=>ΔBAK=ΔBEK
=>góc BEK=góc BAK=90 độ
=>EK vuông góc bC
d: AK=KE
KE<KC
=>AK<KC

a) Xét tam giác BHA và BHE có:
BD chung
\(\widehat{ABD}\)=\(\widehat{EBD}\)(vì BD là phân giác \(\widehat{B}\))
\(\widehat{BHA}\)=\(\widehat{BHE}\)(vì AH vuông góc với Bd tại H)
\(\Rightarrow\)Tam giác BHA=tam giac BHE(c.g.v-g.n.k)
b) Xét Tam giác BDA và tam giác BDE có
BD chung
BA=BE( vì tam giac BHA = tam giac BHE( chứng minh phần a))
ABD=EBD( vì BD là phân giác của\(\widehat{B}\))
\(\Rightarrow\)Tam giác BDA = Tam giác BDE(c.g.c)
\(\Rightarrow\)\(\widehat{BEA}\)=\(\widehat{A}\)= 90o(2 canh tương ứng và \(\widehat{A}\)= 90o)
ED vuông góc với B tại E
d, DA= DE do tam giác ABD = tam giác EBD (Câu b)
=> tam giác DAE cân tại D (đn)
=> ^DAE = ^DEA (tc) (1)
có : AK _|_ BC (gt) ; DE _|_ BC (câu b)
=> DE // AK
=> ^DEA = ^EAK (slt) và (1)
=> ^DAE = ^EAK mà AE nằm giữa AD và AK
=> AE là phân giác của ^CAK (đn)
c, AD = DE
DE < CD do tam giác CDE vuông tại E
=> AD < DC

a: BC=căn 6^2+8^2=10cm
c: Xét ΔABC có
AH,BK là phân giác
AH cắt BK tại O
=>O là tâm đường tròn nội tiếp
=>CO là phân giác của góc ACB

b) Ta có: KI\(\perp\)BC(gt)
AH\(\perp\)BC(gt)
Do đó: KI//AH(Định lí 1 từ vuông góc tới song song)
Suy ra: \(\widehat{HAI}=\widehat{KIA}\)(hai góc so le trong)(1)
Ta có: ΔABK=ΔIBK(cmt)
nên KA=KI(hai cạnh tương ứng)
Xét ΔKAI có KA=KI(cmt)
nên ΔKAI cân tại K(Định nghĩa tam giác cân)
Suy ra: \(\widehat{KAI}=\widehat{KIA}\)(hai góc ở đáy)(2)
Từ (1) và (2) suy ra \(\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAI}=\widehat{CAI}\)
Suy ra: AI là tia phân giác của \(\widehat{HAC}\)(Đpcm)
a) Xét ΔABK vuông tại A và ΔIBK vuông tại I có
BK chung
\(\widehat{ABK}=\widehat{IBK}\)(BK là tia phân giác của \(\widehat{ABI}\))
Do đó: ΔABK=ΔIBK(Cạnh huyền-góc nhọn)

a, xét tam giác ABD và tam giác EBD có : BD chung
góc ABD = góc EBD do BD là pg của góc ABC (gt)
góc DAB = góc DEB = 90
=> tam giác ABD = tam giác EBD (ch-gn)
=> BA = BE (đn)
b, đề sai sao ý
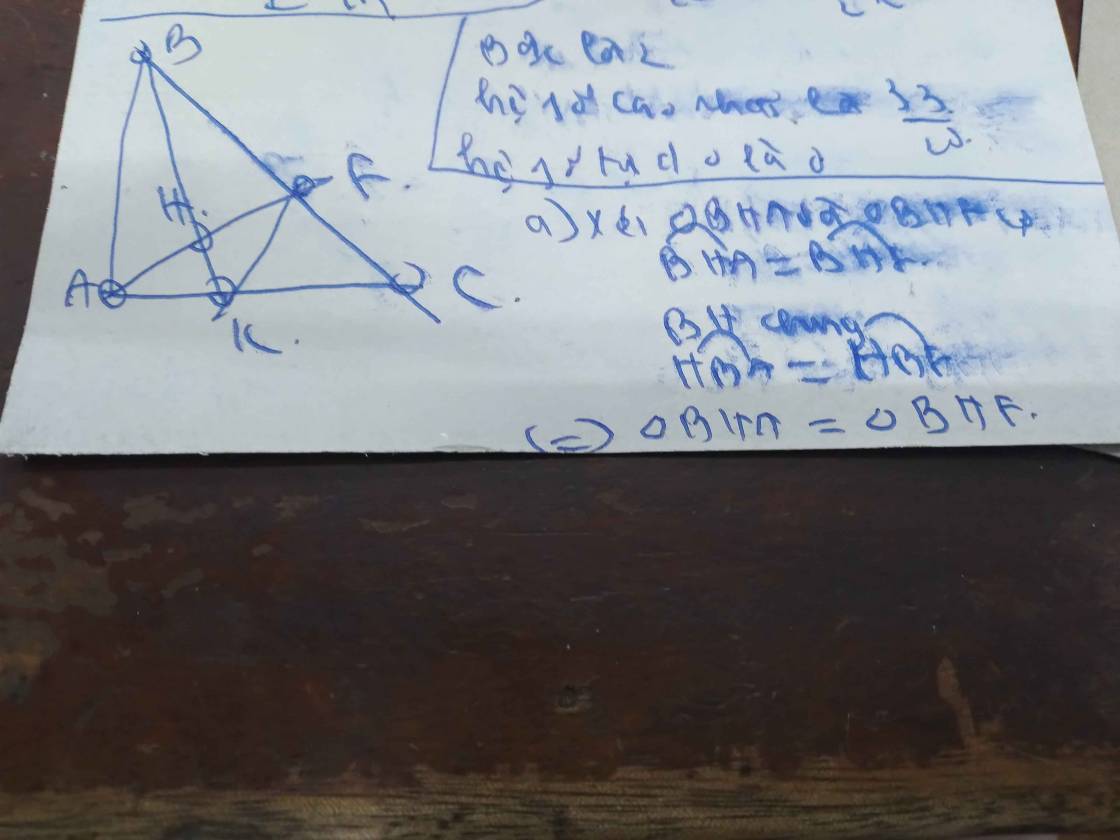
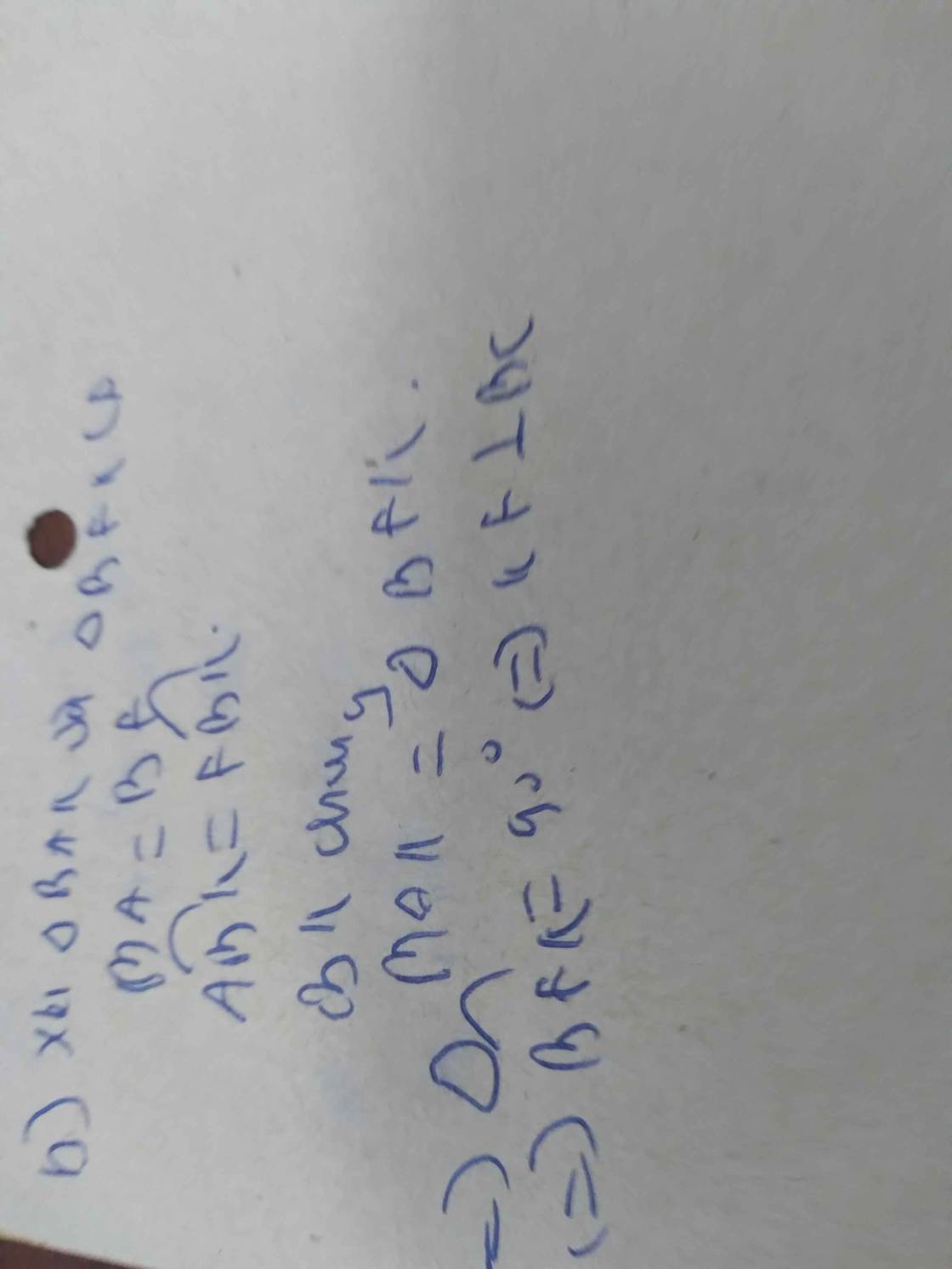
a: Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
góc ABK=góc HBK
=>ΔBAK=ΔBHK
b: ΔBAK=ΔBHK
=>KA=KH
=>ΔKAH cân tại K