Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp (O)
2: góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
góc OAC+góc AFE
=góc AHE+góc OCA
=góc ABC+góc ACB=90 độ
=>FE vuông góc AO

Gọi G là trung điểm AH, I là trung điểm EF, MN là đtb tg ABC
Dễ thấy NG//BC;MG//BC nên M,N,G thẳng hàng
Xét tg AEF và tg HEF có AI;HI là trung tuyến ứng vs ch EF nên \(AI=HI=\dfrac{1}{2}EF\)
Do đó tg AIH cân tại I
Mà IG là trung tuyến (G là trung điểm AH) nên IG là đg cao hay \(IG\perp AH\left(1\right)\)
Xét tg AHB vuông tại H có HM là trung tuyến ứng ch AB nên \(AM=HM=\dfrac{1}{2}AB\)
Do đó tg AHM cân tại M
Mà MG là trung tuyến (G là trung điểm AH) nên MG là đg cao hay \(MG\perp AH\left(1\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow MG//GI\)
Từ đó ta được M;G;I thẳng hàng
Do đó I;M;N thẳng hàng
Vậy trung điểm EF là I nằm trên đt cố định là đường trung bình MN của tg ABC

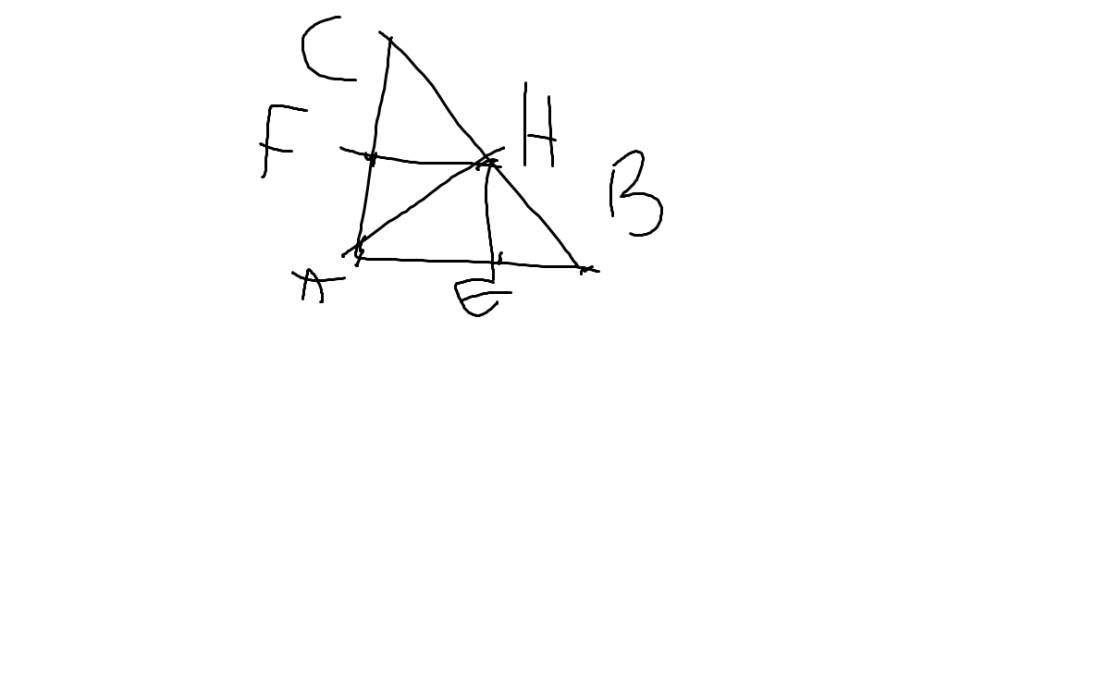
a: ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>HC*4=3^2=9
=>HC=2,25(cm)
BC=BH+CH
=2,25+4
=6,25(cm)
XétΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB^2=2,25\cdot6,25\\AC^2=4\cdot6,25\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{2,25\cdot6,25}=3,75\left(cm\right)\\AC=\sqrt{25}=5\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>HA=EF=3(cm)
c: ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)

a: \(AB=\sqrt{3\cdot15}=3\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{12\cdot15}=6\sqrt{5}\left(cm\right)\)
b: \(\dfrac{HF}{HE}=\dfrac{AE}{AF}=\dfrac{AH^2}{AB}:\dfrac{AH^2}{AC}=\dfrac{AC}{AB}=2\)
=>HF=2HE

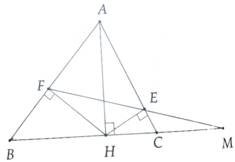
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC

b) Xét ΔMEB và ΔMCF có
\(\widehat{MEB}=\widehat{MCF}\left(=\widehat{AEF}\right)\)
\(\widehat{M}\) chung
Do đó: ΔMEB\(\sim\)ΔMCF(g-g)
Suy ra: \(\dfrac{ME}{MC}=\dfrac{MB}{MF}\)
hay \(ME\cdot MF=MB\cdot MC\)
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)(hai góc tương ứng)

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)
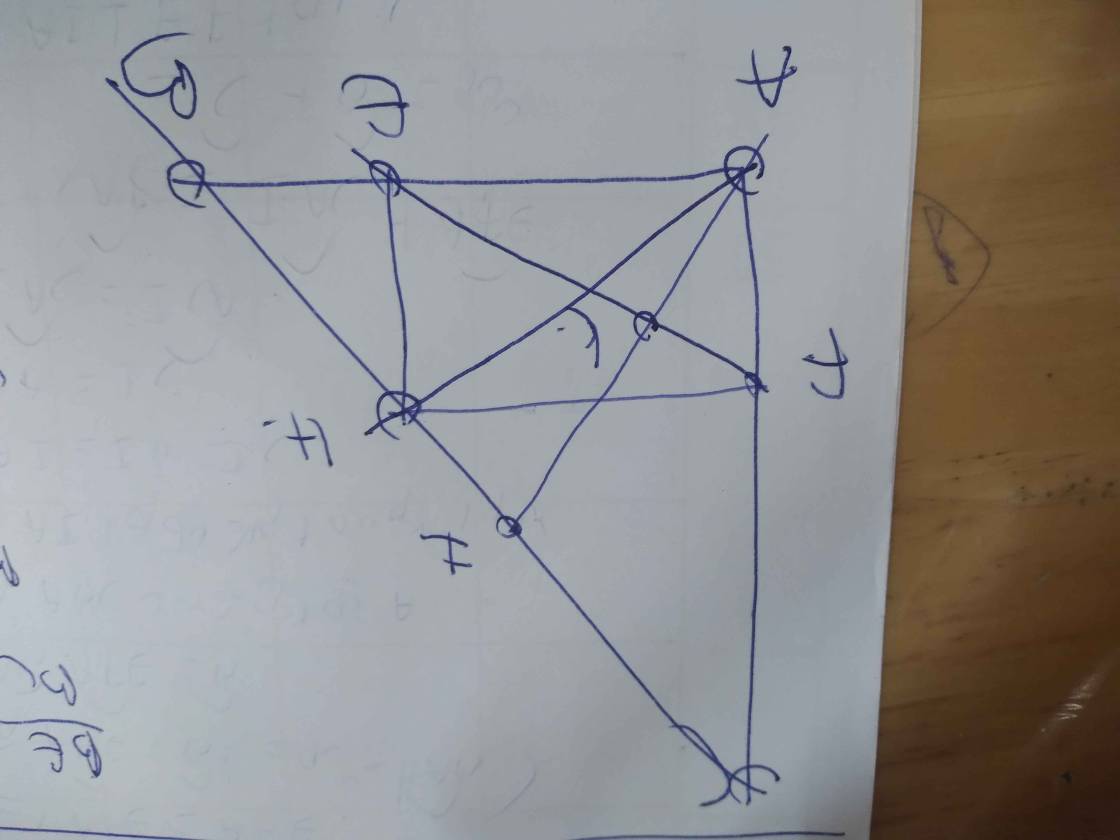
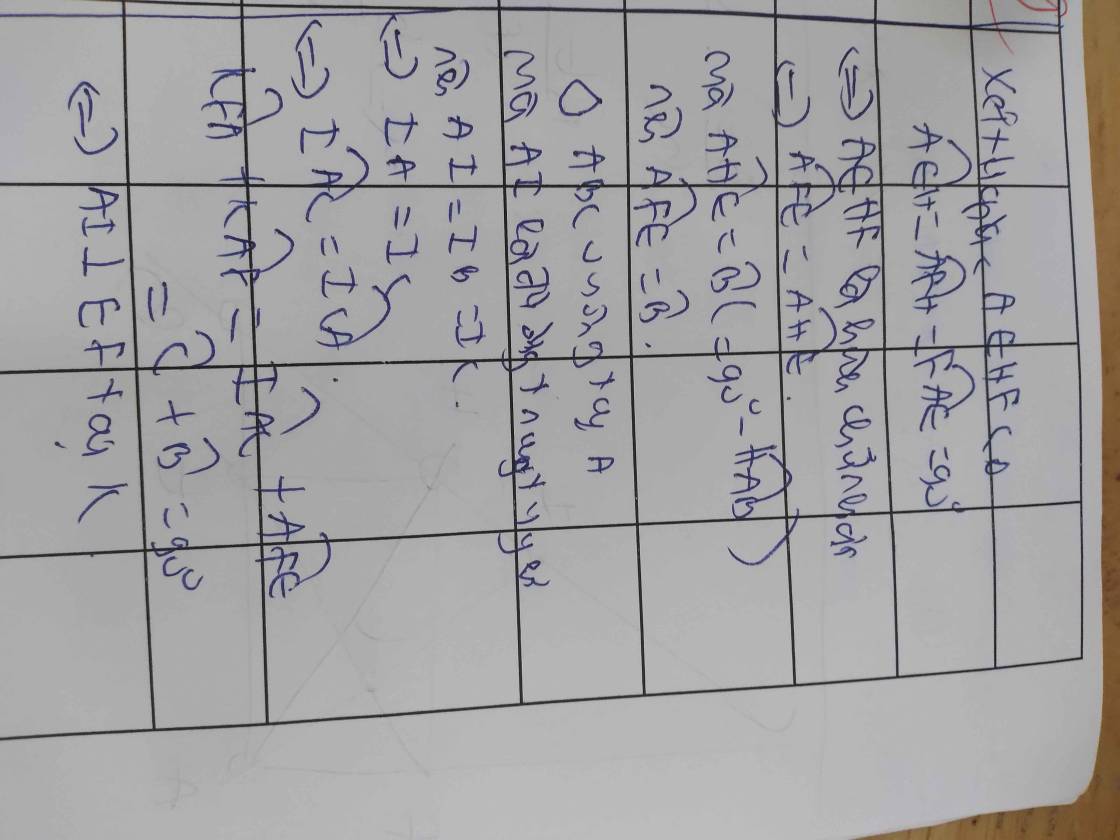
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AH^2=AE\cdot AB\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AH^2=AF\cdot AC\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
\(\Leftrightarrow\frac{AE}{AC}=\frac{AF}{AB}\)
Xét ΔAFE và ΔABC có
\(\frac{AE}{AC}=\frac{AF}{AB}\)(cmt)
\(\widehat{FAE}\) chung
Do đó: ΔAFE∼ΔABC(c-g-c)
Ta có: BC=BH+CH(H nằm giữa B và C)
hay BC=1,6+2,5=4,1cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=1.6\cdot4.1=6.56\\AC^2=2.5\cdot4.1=10.25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{6.56}=\frac{2\sqrt{41}}{5}cm\\AC=\sqrt{10.25}=\frac{\sqrt{41}}{2}cm\end{matrix}\right.\)
Ta có: ΔABC vuông tại A(gt)
\(\Leftrightarrow S_{ABC}=\frac{AB\cdot AC}{2}=\frac{\frac{2\sqrt{41}}{5}\cdot\frac{\sqrt{41}}{2}}{2}=\frac{41}{5}\cdot\frac{1}{2}=4.1cm^2\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh BC, ta được:
\(AH^2=HB\cdot HC=1.6\cdot2.5=4\)
hay \(AH=\sqrt{4}=2cm\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh AB, ta được:
\(AH^2=AE\cdot AB\)
\(\Leftrightarrow2^2=AE\cdot\frac{2\sqrt{41}}{5}\)
\(\Leftrightarrow AE=4:\frac{2\sqrt{41}}{5}=4\cdot\frac{5}{2\sqrt{41}}=\frac{10\sqrt{41}}{41}cm\)
Ta có: ΔAFE∼ΔABC(cmt)
\(\Leftrightarrow\frac{S_{AFE}}{S_{ABC}}=\left(\frac{AE}{AC}\right)^2=\left(\frac{10\sqrt{41}}{41}:\frac{\sqrt{41}}{2}\right)^2\)
\(\Leftrightarrow\frac{S_{AFE}}{4.1}=\left(\frac{10\sqrt{41}}{41}\cdot\frac{2}{\sqrt{41}}\right)^2=\frac{400}{1681}\)
\(\Leftrightarrow S_{AFE}=\frac{400\cdot4.1}{1681}=\frac{40}{41}cm^2\)