Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Xét ΔABC có AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{BH}{CH}=\dfrac{1}{9}\)

1: Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
=>AEDB là tứ giác nội tiếp đường tròn đường kính AB
Tâm I là trung điểm của AB
Bán kính là \(IA=\dfrac{AB}{2}\)
2: Xét ΔDBH vuông tại D và ΔDAC vuông tại D có
\(\widehat{DBH}=\widehat{DAC}\left(=90^0-\widehat{ACB}\right)\)
Do đó: ΔDBH đồng dạng với ΔDAC
=>DB/DA=DH/DC
=>\(DB\cdot DC=DA\cdot DH\)
3: ABDE là tứ giác nội tiếp
=>\(\widehat{ADE}=\widehat{ABE}=\widehat{ABN}\)
Xét (O) có
\(\widehat{ABN}\) là góc nội tiếp chắn cung AN
\(\widehat{AMN}\) là góc nội tiếp chắn cung AN
Do đó: \(\widehat{ABN}=\widehat{AMN}\)
=>\(\widehat{HDE}=\widehat{HMN}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên DE//MN

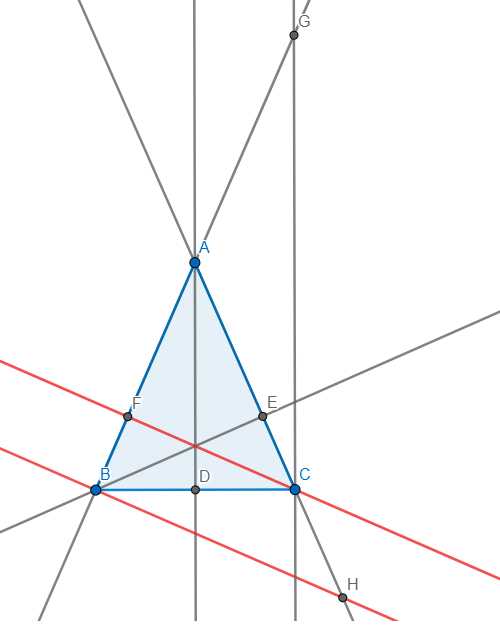
Vì tam giác ABC cân tại A có đường cao AH nên D là trung điểm BC
Từ C kẻ đường thẳng vuông góc với BC cắt AB tại G
\(\Rightarrow CG\parallel AD\) mà D là trung điểm BC \(\Rightarrow A\) là trung điểm BG
nên AD là đường trung bình tam giác BCG \(\Rightarrow AD=\dfrac{CG}{2}\)
\(\Rightarrow2AD=CG\Rightarrow4AD^2=CG^2\)
tam giác BCG vuông tại C có đường cao CF nên áp dụng hệ thức lượng
\(\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{CG^2}=\dfrac{1}{CF^2}\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{4AD^2}=\dfrac{1}{CF^2}\)

a) Xét tứ giác BFEC có
\(\widehat{BFC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
\(\widehat{BFC}=\widehat{BEC}\left(=90^0\right)\)
Do đó: BFEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
=> Đường kính là BC, Tâm là trung điểm của BC
Xét tứ giác BFHD có
\(\widehat{BFH}\) và \(\widehat{BDH}\) là hai góc đối
\(\widehat{BFH}+\widehat{BDH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BFHD là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
=> Đường kính là BH và tâm là trung điểm của BH
Gọi F là điểm đối xứng của CC qua AA
Ta được \(AF=AC=AB\)
\(A,F,C\)thẳng hàng
\(\Rightarrow\Delta BFC\perp B\)
Ta có: \(\Delta ABC\)cân tại A(gt)
\(AD\perp BC\left(gt\right)\)
\(\Rightarrow BD=DC\)
mà \(AF=AC\)
\(\Rightarrow AD\)//\(BF\)mà \(AD=\frac{BF}{2}\)(tính chất đường trung bình)
Áp dụng hệ thức lượng vào \(\Delta BFC\perp B\)đường cao BE ta được:
\(\frac{1}{BE^2}=\frac{1}{BF^2}+\frac{1}{BC^2}\)
\(\Leftrightarrow\frac{1}{BE^2}=\frac{1}{4AD^2}+\frac{1}{BC^2}\)
\(\Leftrightarrow\frac{1}{4k^2}=\frac{1}{4n^2}+\frac{1}{4m^2}\)
\(\Leftrightarrow\frac{1}{k^2}=\frac{1}{n^2}+\frac{1}{m^2}\left(đpcm\right)\)
#Shinobu Cừu