Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì tam giác ABC cân tại A có đường cao AH nên D là trung điểm BC
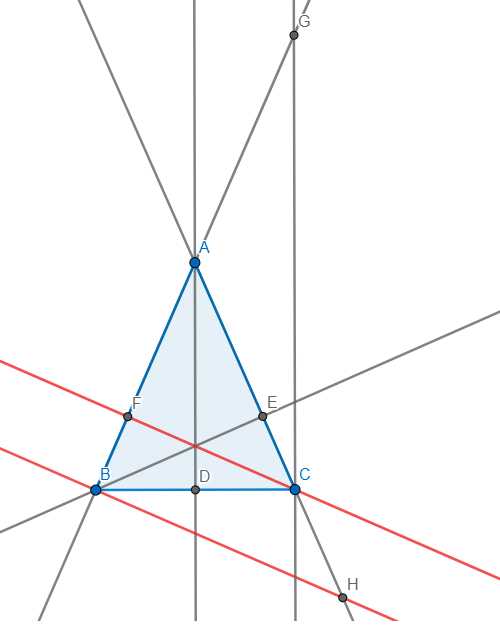
Từ C kẻ đường thẳng vuông góc với BC cắt AB tại G
\(\Rightarrow CG\parallel AD\) mà D là trung điểm BC \(\Rightarrow A\) là trung điểm BG
nên AD là đường trung bình tam giác BCG \(\Rightarrow AD=\dfrac{CG}{2}\)
\(\Rightarrow2AD=CG\Rightarrow4AD^2=CG^2\)
tam giác BCG vuông tại C có đường cao CF nên áp dụng hệ thức lượng
\(\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{CG^2}=\dfrac{1}{CF^2}\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{4AD^2}=\dfrac{1}{CF^2}\)

Cô hướng dẫn nhé.
a) Do ABC là tam giác cân nên AE = AF, AC = AB
Lại có \(\Delta AFC\sim\Delta ABH\left(g-g\right)\Rightarrow\frac{AF}{AB}=\frac{AC}{AH}\Rightarrow AF.AH=AB.AC\Rightarrow AE.AH=AC^2\)
b) Câu này đề ko đúng. Cô sửa lại \(\frac{1}{CF^2}=\frac{1}{BC^2}+\frac{1}{4.AD^2}\)
\(AD.BC=AB.CF\left(=\frac{S_{ABC}}{2}\right)\)
Vậy nên \(VP=\frac{AD^2+\frac{BC^2}{4}}{BC^2.AD^2}=\frac{AD^2+\left(\frac{BC}{2}\right)^2}{CF^2AB^2}=\frac{AD^2+BD^2}{CF^2AB^2}=\frac{AB^2}{CF^2.AB^2}=\frac{1}{CF^2}=VT\)

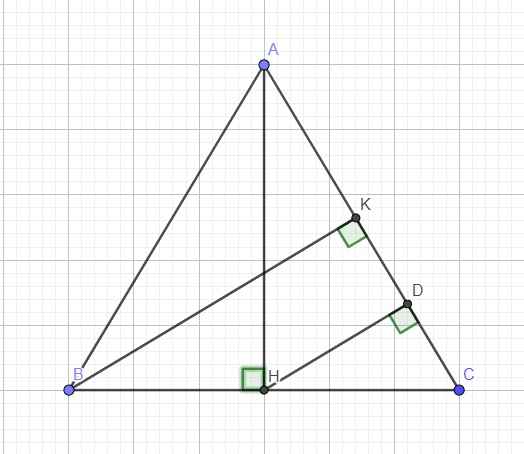
Từ H kẻ \(HD\perp AC\Rightarrow HD||BK\) (cùng vuông góc AC)
Mà ABC cân tại A \(\Rightarrow\) H là trung điểm BC \(\Rightarrow HC=\dfrac{BC}{2}\)
\(\Rightarrow\) HD là đường trung bình tam giác BCK
\(\Rightarrow HD=\dfrac{BK}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACH với đường cao HD ứng với cạnh huyền:
\(\dfrac{1}{HD^2}=\dfrac{1}{AH^2}+\dfrac{1}{CH^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{BK}{2}\right)^2}=\dfrac{1}{AH^2}+\dfrac{1}{\left(\dfrac{BC}{2}\right)^2}\)
\(\Leftrightarrow\dfrac{4}{BK^2}=\dfrac{1}{AH^2}+\dfrac{4}{BC^2}\)
\(\Leftrightarrow\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

a) Do AH là đường cao trong tam giác ABC cân tại A
\(\Rightarrow\) AH cũng là đường trung tuyến trong tam giác ABC
Suy ra H là trung điểm của BC.
mà AH//BD (vì cùng vuông góc với BC)
\(\Rightarrow\) AH là đường trung bình của tam giác DBC
\(\Rightarrow\) 2AH=BD
b)Áp dụng hệ thức trong tam giác vuông có
\(\dfrac{1}{BK^2}=\dfrac{1}{BD^2}+\dfrac{1}{BC^2}=\dfrac{1}{\left(2AH\right)^2}+\dfrac{1}{BC^2}\) \(=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)
Vậy...