Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét △AMB và △AMC có:
AB = AC (△ABC cân)
AM: chung
MB = MC (M: trung điểm BC)
=> △AMB = △AMC (c.c.c)
=> AMB = AMC (2 góc tương ứng)
Mà AMB + AMC = 180o (kề bù)
=> 2AMB = 2AMC = 180o
=> AMB = AMC = 180o : 2 = 90o
=> AM \(\perp\)BC (đpcm)
b) Xét △MBE và MCF có:
MEB = MFC ( = 90o)
MB = MC (M: trung điểm BC)
EBM = FCM (△ABC cân)
=> △MBE = △MCF (ch-gn)
=> ME = MF (2 cạnh tương ứng)
=> △EMF cân tại M (đpcm)
c) Vì △MBE và △MCF => BE = CF
Ta có:
AB = AE + EB
AC = AF + FC
Mà AB = AC (△ABC cân) và EB = FC (cmt)
=> AE = AF
=> △AEF cân tại A
=> AEF = \(\frac{180^o-A}{2}\)(1)
Vì △ABC cân tại A
=> ABC = \(\frac{180^o-A}{2}\)(2)
Từ (1) và (2) => AEF = ABC
Mà hai góc này ở vị trí so le trong
=> EF // BC (đpcm)

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tai F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

a, Vì góc BM là tia phân giác góc BAC nên=> góc BAM= góc MAC
Vì tam giác ABC cân tại A=>AB=AC(t/c)
Xét tam giác AMB và tam giác AMC, ta có:
AB=AC(cmt)
AM(cạnh chung)
góc BAM=góc MAC(cmt)
=>Tam giác AMB=tam giác AMC(c.g.c)
a: Xét ΔAMB và ΔAMC có
AM chung
\(\widehat{BAM}=\widehat{CAM}\)
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
hay ΔAEF cân tại A
c: Ta có: ΔAEF cân tại A
mà AM là đường phân giác
nên AM là đường cao

a) xét ΔABM và ΔACM có
góc B = góc C
AB = AC ( ΔABC cân tại A )
BM=CM ( tính chất các đường của Δ cân từ đỉnh )
=> ΔABM = ΔACM
b) xét ΔBME và ΔCMF có
góc B bằng góc C
BM=CM
=> ΔBME=ΔCMF ( cạnh huyền góc nhọn )
=> FM = EM
=> ΔEMF cân tại M
c) gọi giao của EF và AM là O
ta có BE = CF => AE=AF
=> ΔAEF cân tại A
ta có AM là tia phân giác của góc A
mà O nằm trên AM suy ra AO cũng là tia phân giác của góc A
ta lại có ΔAEF cân tại A
suy ra AO vuông góc với EF
suy ra AM vuông góc với EF
xét ΔAEF và ΔABC có
EF và BC đều cùng vuông góc với AM => EF // BC
a) Xét ΔABM và ΔACM có
AB=AC(ΔABC cân tại A)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)
b) Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
BM=CM(M là trung điểm của BC)
\(\widehat{EBM}=\widehat{FCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEMB=ΔFMC(Cạnh huyền-góc nhọn)
Suy ra: ME=MF(hai cạnh tương ứng)
Xét ΔEMF có ME=MF(cmt)
nên ΔEMF cân tại M(Định nghĩa tam giác cân)

Vì △ABC cân tại A
=> ABC = ACB
Xét △BDM vuông tại D và △CEM vuông tại E
Có: BM = CM (gt)
DBM = ECM
=> △BDM = △CEM (ch-gn)
=> DM = EM (2 cạnh tương ứng)
Xét △AMD vuông tại D và △AME vuông tại E
Có: DM = ME (cmt)
AM là cạnh chung
=> △AMD = △AME (ch-cgv)
=> AD = AE (2 cạnh tương ứng)
Xét △ADE có AD = AE
=> △ADE cân tại A
=> ADC = (180o - A) : 2 (1)
Vì △ABC cân tại A
=> ABC = (180o - A) : 2 (2)
Từ (1), (2) => ADC = ABC
Mà 2 góc này nằm ở vị trí đồng vị
=> DE // BC (dhnb)

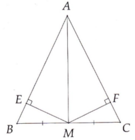
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
c: Xét ΔABC có
AE/AB=AF/AC
Do đó: EF//BC
em cảm ơn . Thanks !