Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tam giác HBA vuông tại H có:
AB2=AH2+BH2(định lí py ta go)
hay 100=AH2+36
=> AH2=64
=> AH=8(cm)
b, Xét tam giác ABH và tam giác ACH có:
góc AHB=góc AHC =90 độ
AB=AC (tam giác ABC cân tại A)
AH chung
=> tam giác ABH = tam giác ACH
c,
Xét tam giác DBH và tam giác ECH có:
BD=CE (gt)
góc DBH= góc ECH (tam giác ABC Cân tại A)
BH=CH (trong tam giác cân, đường cao đồng thời là đường trung tuyến)
=> tam giác DBH=tam giác ECH
=> DH=EH( 2 cạnh tương ứng)
=> tam giác HDE cân tại H
d) Vì AB = AC; BD = CE
mà AB - BD = AD
AC - CE = AE
=> AD = AE
Vì ΔHDE cân
=> H ∈ đường trung trực cạnh DE (1)
Xét ΔADHvàΔAEHcó
AD = AE (cmt)
AH (chung)
DH = HE (cmt)
Do đó: ΔADH=ΔAEH(c−c−c)
=> AD = AE ( hai cạnh tương ứng)
=> ΔADE cân tại A
=> A ∈ đường trung trực cạnh DE (2)
(1); (2) => A,H ∈ đường trung trực cạnh DE
=>AH là đường trung trực cạnh DE
CHÚC BẠN HỌC TỐT

a:Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=> \(BH=\dfrac{BC}{2}=3\left(cm\right)\)
nên AH=4(cm)
b: Ta có: AH là đường trung tuyến ứng với cạnh BC
mà G là trọng tâm của ΔABC
nên A,H,G thẳng hàng
c: XétΔABG và ΔACG có
AB=AC
AG chung
GB=GC
Do đó:ΔABG=ΔACG
Suy ra: \(\widehat{ABG}=\widehat{ACG}\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔAHB=ΔAHC
nên HB=HC
=>HB=BC/2=6(cm)
Xét ΔAHB vuông tại H có
\(AB^2=AH^2+BH^{ }\)
hay AH=8(cm)
c: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của AB
Do đó: MN là đường trung bình
=>MN//BC
d: Xét ΔNCB và ΔMBC có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó: ΔNCB=ΔMBC
Suy ra: \(\widehat{GCB}=\widehat{GBC}\)
hay ΔGBC cân tại G

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường trung tuyến
=>H là trung điểm của BC
=>HB=HC=3cm
=>AH=4cm
b: Ta có: AH là đường trung tuyến
mà AG là đường trung tuyến
và AH,AG có điểm chung là A
nên A,H,G thẳng hàng
c: Xét ΔABG và ΔACG có
AB=AC
\(\widehat{BAG}=\widehat{CAG}\)
AG chung
Do đó: ΔABG=ΔACG

Sửa đề :
a, Tính độ dài cạnh AC
Áp dụng định lí Pytago trong \(\Delta ABC\perp A\)có :
\(AB^2+AC^2=BC^2\)
\(AC^2=BC^2-AB^2=10^2-6^2=64\)
\(AC=\sqrt{64}=8\)
b, Xét \(\Delta AMC\)và \(\Delta BMD\)có :
\(MB=MA\left(gt\right)\)
\(\widehat{AMC}=\widehat{BMD}\)( 2 góc đối đỉnh )
\(MD=MC\left(gt\right)\)
= > \(\Delta AMC=\Delta DMB\)
= > DB = AC = 8 cm ( 2 cạnh tương ứng )
c, thiếu đề bài
ta có :

c. mình đâu có thấy điểm K nào đâu nhỉ

Vì G là trọng tâm ΔABC
⇒AG=2323 AH=2323 18=12(cm)
Mà AG=2GH
⇒GH=AG2AG2 =122122 =6(cm)
BH=HC(do AH là trung tuyến BC)
⇒BH=HC=BC2BC2 =162162 =8(cm)
Xét ΔGHC có:
GH²+HC²=GC²(Định lí Pi-ta-go)
⇒6²+8²=GC²
⇒36+64=GC²
⇒GC²=100=10²
⇒GC=10(cm)
Mà GC=2GI
⇒GI=GC2GC2 =102102=5(cm)
Vậy độ dài cạnh GI là 5cm
d)Ta có:
Theo b) GI=GK
⇒ΔIGK là tam giác cân tại G
{GC=2GIGB=2GK{GC=2GIGB=2GK
Mà GI=GK
⇒GC=GB
⇒ΔGBC là tam giác cân tại G
Ta có:
∠KIG=∠IKG=180∗−∠IGK2180∗−∠IGK2
∠GBC=∠GCB=180∗−∠BGC2180∗−∠BGC2
Mà ∠IGK=∠BGC(đối đỉnh)
⇒∠KIG=∠GCB
Mà 2 góc ở vị trí so le trong
⇒IK=BC
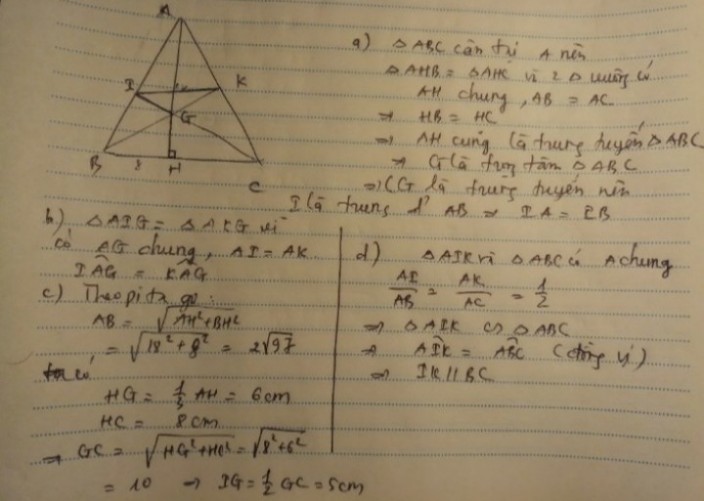
a: BC=8cm nên BH=4cm
\(AH=\sqrt{97-16}=9\left(cm\right)\)