NC
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DP
10 tháng 4 2022
8(%7#2;3786(23#;8%7;23#?3#](?;32%78(23;%(3*2;]34((46(;13846(1;58]63#;?%]3;?85?;3]%68%63(#8%,8632;6%]3;6?%8%,3]?8%23#;8%3#2;%68((14?+^#]?&$%3]3#;(+3]4}](#^&?+(:^?%+(},]?%]}^^?,}#]?,#6?*6*3,#3,](6,(6,3]?73%,]7?%]83#?87%3#,?7%,]?7%3#],?%+78)76}#,^*],)#+/(#})(#]}]7?3#68]7}#(])}7+)](^]74(3+)(+7/4?}(*@?/3#?7^{%79{}7^?#/})7},#(7?:%#?:%*)7#6}?/+?+(7^,;{*?%;{,?+?%^{},?+{#,/%?^&]{#,?,]{?^+3(?^&%3/?(+,3/?^%+?+^#/%3^?}%+#/%?^}?&?%}&#/,?%^+#?}/^+7(}7#+/6?)/}#+76)#/?}7+#/}??7+%/}#??{7#}+%?{,+}#^8^kết quả là *,%^*^#,#61?*%*^^?,#^?%$ chúc bạn học giỏi nhe :)))
DP
10 tháng 4 2022
Bằng 5^57/7,71 cách giải 12:0,1+7/^1-729=5^57/7,71
5^57/7,71-3:3x2+2:4=5^57/7,71
Chúc bạn học giỏi nhe :)))) 👍👍👍👍👍👍👍👍👍
DP
5
TT
23 tháng 9 2016
=1+(2-3-4+5)+3-4-5+6)+...+(200-201-202+203)+204
=1+0+0+...+0+204
=1+204
=205
23 tháng 9 2016
tinh
1+2 -3 -4 +5+3-4-5+6 +4-5-6 +7 + ....+200-201 -202 + 203 + 204 =1+0+...+0+204=1+204=205.
bn k cho mik nha. ^-^ thanks bn trc.
CM
7 tháng 8 2018
Tính nhanh:
a) 1-2-3+4+5-6-7+8+9-10-.......+200+201-202-203
Đặt \(A=\text{1-2-3+4+5-6-7+8+9-10-.......+200+201-202-203}\)
\(A=1+\left(2-3-4+5\right)+\left(6-7-8=9\right)+\left(10-11-12+13\right)+... \)\(+\left(298-299-300+301\right)+302\)
\(A=1+0+0+0+...+0+302\)
\(A=1+302\)
\(A=303\)
Phần B làm sau nha!
DV
0
H9
HT.Phong (9A5)
CTVHS
10 tháng 9 2023
a) Ta có:
\(2^{300}=2^{3\cdot100}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=3^{2\cdot100}=\left(3^2\right)^{100}=9^{100}\)
Mà: \(8< 9\)
\(\Rightarrow8^{100}< 9^{100}\)
\(\Rightarrow2^{300}< 3^{200}\)
b) Ta có:
\(3^{500}=3^{5\cdot100}=\left(3^5\right)^{100}=243^{100}\)
\(7^{300}=7^{3\cdot100}=\left(7^3\right)^{100}=343^{100}\)
Mà: \(243< 343\)
\(\Rightarrow243^{100}< 343^{100}\)
\(\Rightarrow3^{500}< 7^{300}\)
c) Ta có:
\(8^5=\left(2^3\right)^5=2^{3\cdot5}=2^{15}=2\cdot2^{15}\)
\(3\cdot4^7=3\cdot\left(2^2\right)^7=3\cdot2^{2\cdot7}=3\cdot2^{14}\)
Mà: \(2< 3\)
\(\Rightarrow2\cdot2^{14}< 3\cdot2^{14}\)
\(\Rightarrow8^5< 3\cdot4^7\)
d) Ta có:
\(202^{303}=202^{3\cdot101}=\left(202^3\right)^{101}=8242408^{101}\)
\(303^{202}=303^{2\cdot101}=\left(303^2\right)^{101}=91809^{101}\)
Mà: \(8242408>91809\)
\(\Rightarrow8242408^{101}>91809^{101}\)
\(\Rightarrow202^{303}>303^{202}\)
NT
1
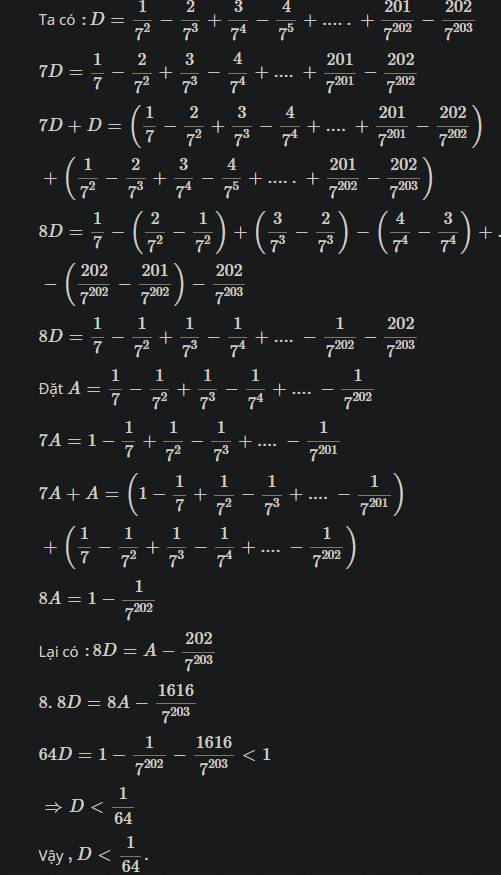
em nên gõ công thức trực quan để được hỗ trợ tốt nhất nhé
D = \(\dfrac{1}{7^2}\) - \(\dfrac{2}{7^3}\) + \(\dfrac{3}{7^4}\) - \(\dfrac{4}{7^5}\) +........+ \(\dfrac{201}{7^{202}}\) - \(\dfrac{202}{7^{203}}\)
7 \(\times\) D = \(\dfrac{1}{7}\) - \(\dfrac{2}{7^2}\) + \(\dfrac{3}{7^3}\) - \(\dfrac{4}{7^4}\) + \(\dfrac{5}{7^5}\) -.......- \(\dfrac{202}{7^{202}}\)
7D +D = \(\dfrac{1}{7}\) - \(\dfrac{1}{7^2}\) + \(\dfrac{1}{7^3}\) - \(\dfrac{1}{7^4}\) + \(\dfrac{1}{7^5}\) -.........-\(\dfrac{1}{7^{202}}\) - \(\dfrac{202}{7^{203}}\)
D = ( \(\dfrac{1}{7}\) - \(\dfrac{1}{7^2}\) + \(\dfrac{1}{7^3}\) - \(\dfrac{1}{7^4}\) + \(\dfrac{1}{7^5}\) -.........-\(\dfrac{1}{7^{202}}\) - \(\dfrac{202}{7^{203}}\)) : 8
Đặt B = \(\dfrac{1}{7}\) - \(\dfrac{1}{7^2}\) + \(\dfrac{1}{7^3}\) - \(\dfrac{1}{7^4}\) + \(\dfrac{1}{7^5}\) -........+\(\dfrac{1}{7^{201}}\).-\(\dfrac{1}{7^{202}}\)
7 \(\times\) B = 1 - \(\dfrac{1}{7}\)+\(\dfrac{1}{7^2}\) - \(\dfrac{1}{7^3}\) + \(\dfrac{1}{7^4}\) - \(\dfrac{1}{7^5}\) +.........- \(\dfrac{1}{7^{201}}\)
7B + B = 1 - \(\dfrac{1}{7^{202}}\)
B = ( 1 - \(\dfrac{1}{7^{202}}\)) : 8
D = [ ( 1 - \(\dfrac{1}{7^{202}}\)): 8 - \(\dfrac{202}{7^{203}}\)] : 8
D = \(\dfrac{1}{64}\) - \(\dfrac{1}{64.7^{202}}\) - \(\dfrac{202}{7^{203}.8}\) < \(\dfrac{1}{64}\)