Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔCED vuông tại E có \(EC^2+ED^2=CD^2\)
=>\(EC^2=CD^2-ED^2\)
Xét ΔEDB vuông tại E có \(EB^2+ED^2=BD^2\)
=>\(EB^2=BD^2-ED^2\)
Xét ΔDAB vuông tại A có \(DA^2+AB^2=DB^2\)
=>\(EB^2=BD^2-ED^2=DA^2+AB^2-ED^2\)
\(EB^2-EC^2\)
\(=DA^2+AB^2-ED^2-CD^2+ED^2\)
\(=AB^2+CD^2-CD^2=AB^2\)

Bạ xem bài làm của bạn Nguyễn Võ Thảo Vy ở đường link sau:
Câu hỏi của Nguyễn Desmond - Toán lớp 8 - Học toán với OnlineMath
TL
Bn xem bài của Nguyễn Thảo Vy ở quản lí đã đưa ra nha
Hok tốt nghen
Nhớ k mik nha

Hướng dẫn:
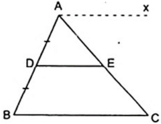
Do DE//BC theo giả thiết nên vẽ thêm Ax//DE thì
Ax//DE//BC ( 1 )
Vì D là trung điểm của AB nên AD = BD ( 2 )
Từ ( 1 ), ( 2 ) suy ra ba đường Ax, DE, BC là ba đường song song cách đều nên nó chắn trên đường thẳng AC hai đoạn thẳng liên tiếp bằng nhau là AE = EC.

a) Xét tứ giác AEHD có \(\widehat{A}=\widehat{AEH}=\widehat{ADH}=90^0\)
=> tứ giác AEHD là HCN
=> AH = DE
b) Gọi O là giao điểm của AM và DE
Xét t/giác ABC vuông tại A có AM là đường trung tuyến
=> AM = BM = CM = 1/2BC
=> t/giác AMC cân tại M => \(\widehat{A1}=\widehat{C}\) (1)
Ta có: \(\widehat{C}+\widehat{H2}=90^0\)(phụ nhau)
\(\widehat{H1}+\widehat{H2}=90^0\)(phụ nhau)
=> \(\widehat{C}=\widehat{H1}\) (2)
Từ (1) và (2) => \(\widehat{H1}=\widehat{A1}\)
Do AEHD là HCN => \(\widehat{OEA}=\widehat{HAE}\)
Ta có: \(\widehat{A1}+\)\(\widehat{E1}+\widehat{A}1=\widehat{H1}+\widehat{HAE}=90^0\)
=> t/giác AOE vuông => \(\widehat{AOE}=90^0\) => AM vuông góc với DE
c) Ta có: SABM = AH. BM/2
SAMC = AH. MC/2
Mà BM = MC => SABM = SAMC
Ta có: SABC = SABM + SAHC = 2S.AMC