Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
a) Có: \(\Delta\)ABC vuông tại A và ^ACB = 40\(^o\)
=> ^ABC = 90\(^o\)- 40\(^o\)=50\(^o\)
b ) Xét \(\Delta\)AMB và \(\Delta\)EMC có: AM = ME ; BM = MC ( gt ) ; ^AMB = ^EMC ( đối đỉnh )
=> \(\Delta\)AMB = \(\Delta\)EMC
=> ^ABM = ^ECM => ^ABC = ^BCE => AB //EC
c) \(\Delta\)ABC vuông tại A có AM là trung tuyến
=> AM = BM= CM =ME
=> \(\Delta\)MEC cân tại M => ^MEC =^ MCE mà ^MEC = ^ECK ( so le trong ) và ^KEC + ^ECK = 90\(^o\)
=> ^^MCE + ^KEC = 90\(^o\)
Ta lại có: AB //EC => ^ECA = 90 \(^o\)=> ^BCA +^ BCE = 90\(^o\)=> ^BCA + ^MCE = 90\(^o\)
=> ^BCA = ^KEC

a: Xét ΔAMB và ΔEMC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)
MB=MC
Do đó: ΔAMB=ΔEMC
b: Ta có: ΔAMB=ΔEMC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
Ta có: AB//CE
AB\(\perp\)AC
Do đó: CE\(\perp\)AC
c: Xét ΔECA vuông tại C và ΔBAC vuông tại A có
EC=BA(ΔMCE=ΔMBA)
AC chung
Do đó: ΔECA=ΔBAC
=>EA=BC
mà EA=2AM
nên BC=2AM

a: Xét ΔMAB và ΔMEC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMEC
b: Ta có: ΔMAB=ΔMEC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//EC
c: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMEB
=>\(\widehat{MAC}=\widehat{MEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BE
Ta có: AB//EC
AB\(\perp\)AC
Do đó: EC\(\perp\)AC
Ta có: AC//BE
AC\(\perp\)EC
Do đó: BE\(\perp\)EC
=>ΔBEC vuông tại E

b) ΔACE cân
Trả lời:
Xét ΔACH và ΔECH có :
AH = HE (gt)
AHCˆ=EHCˆ(=90o)
HC: chung
=> ΔACH=ΔECH (cạnh huyền-cạnh góc vuông)
=> CA= CE (2 cạnh tương ứng)
Xét ΔCAE có :
AC = CE (cmt)
=> ΔCAE cân tại C
~Học tốt!~

a: Xét ΔAMB và ΔCMD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔAMB=ΔCMD

Lời giải:
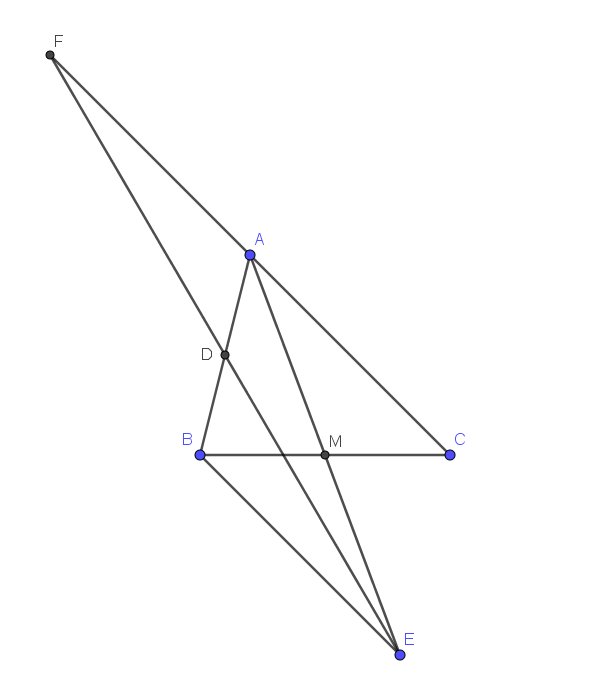
a. Xét tam giác $AMC$ và $EMB$ có:
$AM=ME$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{AMC}=\widehat{EMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle EMB$ (c.g.c)
$\Rightarrow AC=EB$
b. Xét tam giác $AFD$ và $BED$ có:
$FD=ED$
$AD=BD$ (do $D$ là trung điểm $AB$)
$\widehat{ADF}=\widehat{BDE}$ (đối đỉnh)
$\Rightarrow \triangle AFD=\triangle BED$ (c.g.c)
$\Rightarrow AF=BE$
Mà theo phần a thì $AC=BE$ nên $AF=AC$

b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC