Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: (SC;(SAB))=(SC;SB)=góc BSC
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
\(SB=\sqrt{a^2+\left(a\sqrt{3}\right)^2}=2a\)
\(cosBSC=\dfrac{SB^2+SC^2-BC^2}{2\cdot SB\cdot SC}=\dfrac{4a^2+5a^2-a^2}{2\cdot2a\cdot a\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
=>góc BSC=27 độ
b: (SO;(SAB))=(SO;SK)(OK vuông góc AB tại K)
Xét ΔABC có OK//BC
nên OK/BC=AK/AB=AO/AC=1/2
=>OK=a/2; AK=1/2a
\(SK=\sqrt{SA^2+AK^2}=\sqrt{3a^2+\dfrac{1}{4}a^2}=\dfrac{a\sqrt{13}}{2}\)
\(SO=\sqrt{SA^2+AO^2}=\sqrt{3a^2+\dfrac{1}{2}a^2}=\dfrac{a\sqrt{14}}{2}\)
OK=a/2
\(cosOSK=\dfrac{SO^2+SK^2-OK^2}{2\cdot SO\cdot SK}=\dfrac{\dfrac{14}{4}a^2+\dfrac{13}{4}a^2-\dfrac{1}{4}a^2}{2\cdot\dfrac{a\sqrt{14}}{2}\cdot\dfrac{a\sqrt{13}}{2}}=\dfrac{\sqrt{182}}{14}\)
=>góc OSK=16 độ
c: (SA;SBD)=(SA;SO)(AO vuông góc BD) tại O
=góc ASO
\(SO=\sqrt{SA^2+AO^2}=\sqrt{3a^2+\dfrac{1}{2}a^2}=\dfrac{a\sqrt{14}}{2}\)
SA=a căn 3
AO=a*căn 2/2
\(cosASO=\dfrac{SA^2+SO^2-AO^2}{2\cdot SA\cdot SO}=\dfrac{\sqrt{42}}{7}\)
=>góc ASO=22 độ

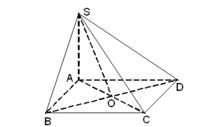
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
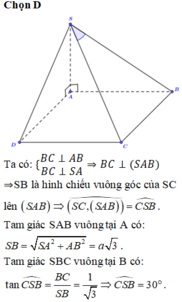
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)

a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
c: (SC;(SAD))=(SC;SD)=góc CSD
Vì ABCD là hình vuông nên \(AC=a\sqrt{2}\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
\(SD=\sqrt{SA^2+AD^2}=2a\)
\(cosCSD=\dfrac{SC^2+SD^2-CD^2}{2\cdot SC\cdot SD}=\dfrac{5a^2+4a^2-a^2}{2\cdot a\sqrt{5}\cdot2a}=\dfrac{2\sqrt{5}}{5}\)=>\(\widehat{CSD}\simeq27^0\)

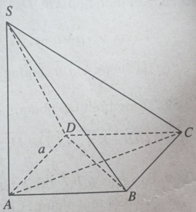
a) (BD ⊥ SA & BD ⊥ AC ⇒ BD ⊥ (SAC)
⇒ BC ⊥ SC.
b) (BC ⊥ SA & BC ⊥ AB ⇒ BC ⊥ (SAB)
⇒ (SBC) ⊥ (SAB).
c) + Xác định góc α giữa đường thẳng SC và mp(ABCD):
(C ∈(ABCD) & SA ⊥ (ABCD) ⇒ ∠[(SC,(ABCD))] = ∠(ACS) = α
+ Tính góc:
Tam tam giác vuông SCA, ta có:
tanα = SA/AC = √3/3 ⇒ α = 30 o .

a: (SAB) giao (ABCD)=AB
SA vuông góc AB, SA thuộc (SAB)
AD vuông góc AB, AD thuộc (ABCD)
=>((SAB);(ABCD))=góc SAD=90 độ

Đáp án D
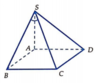
Ta có 
Vậy SB là hình chiếu vuông góc của SC lên mặt phẳng (SAB)
![]()
![]()
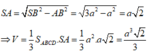

Gọi M là trung điểm AB \(\Rightarrow AM=a\Rightarrow ADCM\) là hình vuông
\(\Rightarrow CM\perp AB\Rightarrow CM\perp\left(SAB\right)\)
\(\Rightarrow\widehat{CSM}\) là góc giữa SC và (SAB)
\(SM=\sqrt{SA^2+AM^2}=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(tan\widehat{CSM}=\dfrac{CM}{SM}=\dfrac{a}{a\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{CSM}\approx35^015'\)
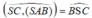
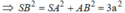
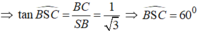
(SC;(SAB))=(SC;SB)=góc BSC
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
\(SB=\sqrt{a^2+\left(a\sqrt{3}\right)^2}=2a\)
\(cosBSC=\dfrac{SB^2+SC^2-BC^2}{2\cdot SB\cdot SC}=\dfrac{4a^2+5a^2-a^2}{2\cdot2a\cdot a\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
=>góc BSC=27 độ