Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi M, N lần lượt là trung điểm của AB, CD, H là chân đường vuông góc kẻ từ M tới SN. Khi đó SM ⊥ (ABCD). Vì AB // CD nên AB // (ABCD), do đó d(A, (SCD)) = d(M, (SCD)) = MH
Ta có
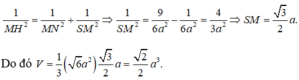

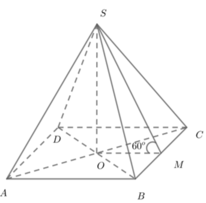
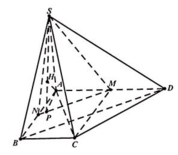
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Gọi M là trung điểm AB \(\Rightarrow AB\perp OM\Rightarrow AB\perp\left(SOM\right)\)
\(\Rightarrow\widehat{SMO}\) là góc giữa mặt bên và đáy hay \(\widehat{SMO}=60^0\)
\(SO=OM.tan\widehat{SMO}=\dfrac{a}{2}.tan60^0=\dfrac{a\sqrt{3}}{2}\)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.a^2=\dfrac{a^3\sqrt{3}}{6}\)

Đáp án B
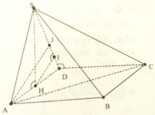
Gọi H là trung điểm của AD, vì ΔASD cân ở S nên SH ⊥ AD.
Vì (SAD)⊥(ABCD) nên SH ⊥ (ABCD). Kẻ HI ⊥ SD.
Vì DC ⊥ AD, DC ⊥ SH nên DC ⊥ (SAD). Do đó DC ⊥ HI.
Kết hợp với HI ⊥ SD, suy ra HI ⊥ (SDC).
Vì AB // (SDC) nên d(B; (SDC)) = d(A; (SDC)) = 2HI
Ta có
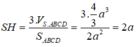
Ta lại có


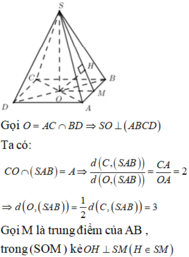
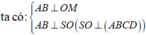
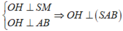
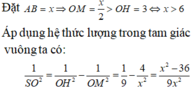
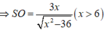
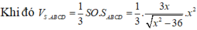
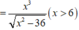
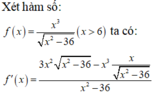
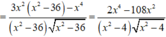
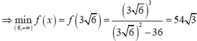
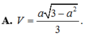

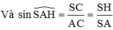
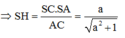
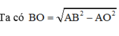
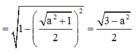
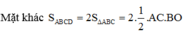
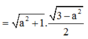
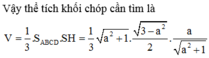
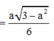


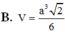
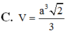
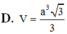
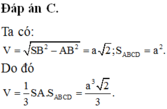
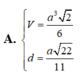
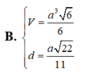
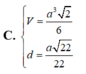
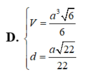
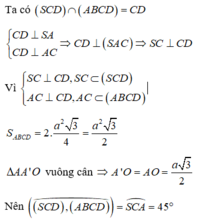
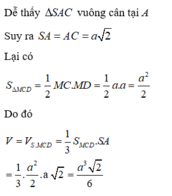
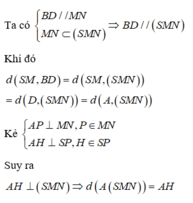

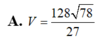
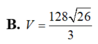
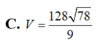
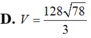
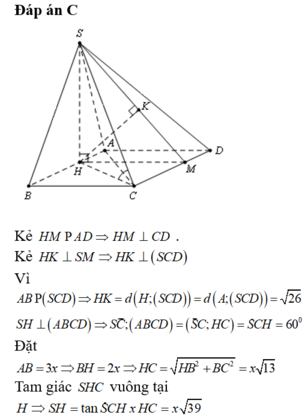

Đáp án: D
Gọi độ dài cạnh đáy là x (x >0).
Gọi M là trung điểm của CD
⇒ d O , ( S C D ) = O H
Ta lại có
⇒ S O = a x x 2 - 4 a 2
Kết luận V S . A B C D = 1 3 x 2 . a x x 2 - 4 a 2
Thể tích khối chóp S.ABCD nhỏ nhất
⇔ f ( x ) = x 3 x 2 - 4 a 2 n h ỏ n h ấ t v ớ i x > 2 a
Lại có f ' ( x ) = 2 x 4 - 12 a 2 x 2 ( x 2 - 4 a 2 ) 3
vẽ bảng biến thiên khi đó
V S . A B C D = 1 3 ( a 6 ) 2 . a . a 6 2 a 2 = 2 3 a 3