Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔANM và ΔABC có
AN/AB=AM/AC
\(\widehat{NAM}\) chung
Do đó: ΔANM\(\sim\)ΔABC

b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB\cdot AC=BC\cdot AH\)

CD=8cm=1/2BC
=>D là trung điểm của BC
Xét ΔABC có AD là trung tuyến
nên \(AD=\sqrt{\dfrac{9^2+12^2}{2}-\dfrac{16^2}{4}}=\dfrac{\sqrt{194}}{2}\left(cm\right)\)

* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
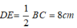
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D

a: Xét ΔABN và ΔACM có
AB/AC=AN/AM
góc A chung
=>ΔABN đồng dạng với ΔACM
b: ΔABN đồng dạng với ΔACM
=>BN/CM=AB/AC=8/16=1/2
=>BN=5cm