Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(u_3=u_1\cdot q^2=9\left(1\right)\)
\(u_6=u_1\cdot q^5=243\left(2\right)\)
\(\dfrac{\left(1\right)}{\left(2\right)}=\dfrac{1}{q^3}=\dfrac{9}{243}=\dfrac{1}{27}\)
\(\Rightarrow q^3=27\)
\(\Rightarrow q=3\)
\(u_1=\dfrac{u_3}{q^2}=\dfrac{9}{3^2}=1\)\(\text{}\)
\(S_{10}=\dfrac{u_1\left(1-q^{10}\right)}{1-q}=\dfrac{1\left(3^{10}-1\right)}{3-1}=29524\)
tìm các số hạng của 1 cấp số nhân có 5 số hạng biết u1=3 và số hạng cuối là 243

Chọn đáp án A
Gọi u 1 , d lần lượt là số hạng đầu và công sai của cấp số cộng
Ta có: u 5 = - 15 u 20 = 60 .
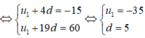
Vậy S 10 = 10 2 . ( 2 u 1 + 9 d ) = - 125

\(\left\{{}\begin{matrix}u_1+d=3\\u_1+9d=-15\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=\dfrac{21}{4}\\d=-\dfrac{9}{4}\end{matrix}\right.\)
\(S_{20}=\dfrac{21}{4}.20+\dfrac{19.20}{2}.\left(-\dfrac{9}{4}\right)=-\dfrac{645}{2}\)

Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77

Phương pháp:
S n = n u 1 + n ( n - 1 ) d 2
Cách giải:
Ta có:
![]()
⇒ S 20 = n u 1 + n ( n - 1 ) 2 d = - 320
Chọn C

Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
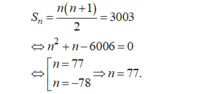

Ta có: u 2 + u 23 = 60 ⇔ u 1 + d + u 1 + 22 d = 60 ⇔ 2 u 1 + 23 d = 60.
Khi đó S 24 = n 2 . 2 u 1 + ( n − 1 ) d = 24 2 2 u 1 + 23 d = 12.60 = 720.
Chọn đáp án C
Chọn đáp án A
Gọi u1, d lần lượt là số hạng đầu và công sai của cấp số cộng
Ta có: u 5 = - 15 u 20 = 60
Vậy S 10 = 10 2 . ( 2 u 1 + 9 d ) = - 125