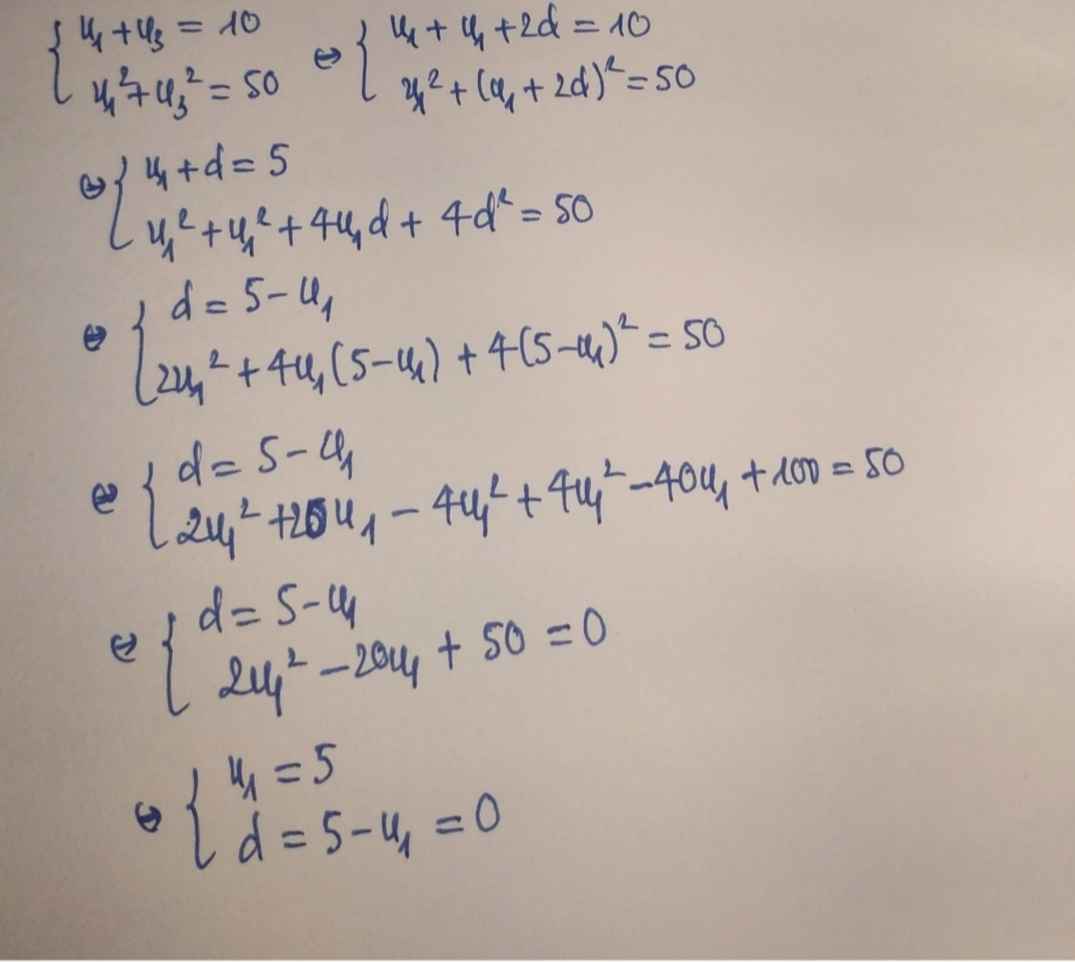Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:
\(S_8=\dfrac{u_1\cdot\left(1-q^8\right)}{1-q}=\dfrac{2048\cdot\left(1-\left(\dfrac{5}{4}\right)^8\right)}{1-\dfrac{5}{4}}\)
\(=-8192\left(1-\left(\dfrac{5}{4}\right)^8\right)\)
2:
\(u2=u1\cdot q\)
=>\(q=\dfrac{3}{-1}=-3\)
\(S_{10}=\dfrac{u1\left(1-q^{10}\right)}{1-q}=\dfrac{-1\cdot\left(1-\left(-3\right)^{10}\right)}{1-\left(-3\right)}\)
\(=\dfrac{-1}{4}\left(1-3^{10}\right)\)

Câu 2:
\(\left\{{}\begin{matrix}u_1+u_5-u_3=10\\u_1+u_6=17\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+u_1+4d-u_1-2d=10\\u_1+u_1+5d=17\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+2d=10\\2u_1+5d=17\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2u_1+4d=20\\2u_1+5d=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2u_1+4d-2u_1-5d=20-17\\2u_1+5d=17\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-d=3\\2u_1+5d=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=-3\\2u_1=17-5d=17+5\cdot3=32\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1=16\\d=-3\end{matrix}\right.\)
Câu 1:
Để a,b,c lập thành cấp số cộng thì
\(\left[{}\begin{matrix}a+c=2b\\a+b=2c\\b+c=2a\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x+1+x^2-1=2\cdot\left(3x-2\right)\\x+1+3x-2=2\left(x^2-1\right)\\x^2-1+3x-2=2\left(x+1\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x^2+x-6x+4=0\\2x^2-2=4x-1\\x^2+3x-3-2x-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x^2-5x+4=0\\2x^2-4x-1=0\\x^2+x-5=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(x-1\right)\left(x-4\right)=0\\2x^2-4x-1=0\\x^2+x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\in\left\{1;4\right\}\\x\in\left\{\dfrac{2+\sqrt{6}}{2};\dfrac{2-\sqrt{6}}{2}\right\}\\x\in\left\{\dfrac{-1+\sqrt{21}}{2};\dfrac{-1-\sqrt{21}}{2}\right\}\end{matrix}\right.\)

1: u3=-3 và u9=29
=>u1+2d=-3 và u1+8d=29
=>-6d=-32 và u1+2d=-3
=>d=16/3 và u1=-3-2d=-3-32/3=-41/3
2: \(S_{20}=\dfrac{20\cdot\left[2\cdot u1+19\cdot d\right]}{2}=10\cdot\left(-5\cdot2+19\cdot3\right)\)
=10(57-10)
=10*47=470

1: u2=4 và u4=10
=>u1+d=4 và u1+3d=10
=>2d=6 và u1+d=4
=>d=3 và u1=1
\(S_{10}=\dfrac{10\cdot\left(2\cdot1+9\cdot3\right)}{2}=5\cdot\left(2+27\right)=145\)
2:
u3=6 và u5=16
=>u1+2d=6 và u1+4d=16
=>2d=10 và u1+2d=6
=>d=5 và u1=6-2*5=-4
\(S_{12}=\dfrac{12\cdot\left(2\cdot\left(-4\right)+11\cdot5\right)}{2}=6\cdot\left(-8+55\right)=6\cdot47=282\)

a.
\(\left\{{}\begin{matrix}u_1+\left(u_1+4d\right)-\left(u_1+2d\right)=10\\\left(u_1+d\right)+\left(u_1+4d\right)=7\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1+2d=10\\2u_1+5d=7\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=36\\d=-13\end{matrix}\right.\)
b.
\(\left\{{}\begin{matrix}u_1+d+u_1+3d=5\\u_1^2+\left(u_1+4d\right)^2=25\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4d=5-2u_1\\u_1^2+\left(u_1+4d\right)^2=25\end{matrix}\right.\)
\(\Rightarrow u_1^2+\left(u_1+5-2u_1\right)^2=25\)
\(\Rightarrow u_1^2+u_1^2-10u_1+25=25\)
\(\Rightarrow\left[{}\begin{matrix}u_1=0\Rightarrow d=\dfrac{5}{4}\\u_1=5\Rightarrow d=-\dfrac{5}{4}\end{matrix}\right.\)

\(\left\{{}\begin{matrix}u_1+u_3=10\\\left(u_1+u_3\right)^2-2u_1u_3=50\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1+u_3=10\\u_1u_3=25\end{matrix}\right.\)
Theo Viet đảo, \(u_1\) và \(u_3\) là nghiệm:
\(x^2-10x+25=0\Rightarrow x=5\)
\(\Rightarrow u_1=u_3=5\)
\(\Rightarrow\left\{{}\begin{matrix}u_1=5\\u_1q^2=5\end{matrix}\right.\) \(\Rightarrow q^2=1\Rightarrow q=\pm1\)

\(\Leftrightarrow\left\{{}\begin{matrix}u_1-u_1-2q+u_1+4q=65\\u_1+u_1+6q=325\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1+2q=65\\2u1+6q=325\end{matrix}\right.\)
=>u1=-130; q=195/2
`u_n = u_1 + (n-1).d`
`{(u_1-u_3+u_5=65),(u_1+u_7=325):}`
`<=>{(u_1-u_1-2d+u_1+4d=65),(u_1+u_1+6d=325):}`
`<=>{(u_1+2d=65),(2u_1+6d=325):}`
`<=>{(u_1=-130),(u_2=195/2):}`

a: u4=4 và u6=8
=>u1+3d=4 và u1+5d=8
=>-2d=-4 và u1+3d=4
=>d=2 và u1=4-3d=-2
b: u1-u3+u5=10 và u1+u6=17
=>u1-u1-2d+u1+4d=10 và u1+u1+5d=17
=>u1+2d=10 và 2u1+5d=17
=>u1=16 và d=-3
c: u1+u2=5 và u3*u5=91
=>u1+u1+d=5 và (u1+2d)(u1+4d)=91
=>2u1+d=5 và (u1+2d)(u1+4d)=91
=>d=5-2u1 và (u1+10-4u1)(u1+20-8u1)=91
=>d=5-2u1 và (-3u1+10)(-7u1+20)=91
(-3u1+10)(-7u1+20)=91
=>21u1^2-60u1-70u1+200=91
=>21u1^2-130u1+109=0
=>u1=1 hoặc u1=109/21
Khi u1=1 thì d=5-2u1=5-2=3
Khi u1=109/21 thì d=5-2u1=5-218/21=-113/21