Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77

Đề không cho sẵn dãy tăng à? Vậy phải chứng minh nó tăng trước
\(u_{n+1}=\dfrac{u_n^2+2018u_n+1}{2020}\)
\(u_{n+1}-u_n=\dfrac{u_n^2+2018u_n+1}{2020}-u_n=\dfrac{\left(u_n-1\right)^2}{2020}\ge0\) \(\Rightarrow\) dãy tăng và không bị chặn trên \(\Rightarrow lim\left(u_n\right)=+\infty\)
\(\Rightarrow2020u_{n+1}=u_n^2+2018u_n+1\)
\(\Leftrightarrow2020u_{n+1}-2020=u_n^2+2018u_n-2019\)
\(\Leftrightarrow2020\left(u_{n+1}-1\right)=\left(u_n+2019\right)\left(u_n-1\right)\)
\(\Rightarrow\dfrac{1}{2020\left(u_{n+1}-1\right)}=\dfrac{1}{\left(u_n+2019\right)\left(u_n-1\right)}=\dfrac{1}{2020}\left(\dfrac{1}{u_n-1}-\dfrac{1}{u_n+2019}\right)\)
\(\Rightarrow\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Thế n=1;2;...;n ta được:
\(\dfrac{1}{u_1+2019}=\dfrac{1}{u_1-1}-\dfrac{1}{u_2-1}\)
\(\dfrac{1}{u_2+2019}=\dfrac{1}{u_2-1}-\dfrac{1}{u_3-1}\)
...
\(\dfrac{1}{u_n+2019}=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}\)
Cộng vế: \(S_n=\dfrac{1}{u_n-1}-\dfrac{1}{u_{n+1}-1}=\dfrac{1}{2018}-\dfrac{1}{u_{n+1}-1}\)
\(\Rightarrow\lim\left(S_n\right)=\dfrac{1}{2018}-\dfrac{1}{\infty}=\dfrac{1}{2018}\)

1. Gọi công bội của csn đó là $q$ thì:
$u_6=q^4u_2$
$\Leftrightarrow 32=q^4.2\Leftrightarrow q^4=16$
$\Leftrightarrow q=\pm 2$
2.
$u_{2019}=q^{2018}u_1=2.3^{2018}$

Chọn C.
Đặt a = u1 thì u22 + u32 + u42 = (a + d)2 + (a + 2d)2 + (a + 3d2 = 3a2 – 36a + 126 = 3(a – 6)2 + 18 ≥ 18 với mọi a.
Dấu bằng xảy ra khi a – 6 = 0 hay a = 6.
Suy ra 6 = u1.
Ta có 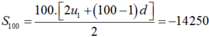

Đáp án A
Phép tịnh tiến biến (d) thành chính nó là phép tịnh tiến theo vectơ chỉ phương của (d)
v → ( 2019 ; − 2018 ) = k u → = 2019 k ; k m => k = 1 m = – 2018
=>có một giá trị m = – 2018 để biến (d) thành chính nó

Chọn C
Sử dụng tính chất của cấp số cộng và công thức tính tổng n số hạng đầu của cấp số cộng là
S n = n . u 1 + n ( n - 1 ) 2 . d
Chọn A
Phương pháp:
Cấp số cộng ( u n ) có công sai d
u n = u 1 + ( n - 1 ) d
d = u n - u 1 n - 1
Cách giải:
u 3 2 + u 4 2 = ( u 1 + 2 d ) 2 + ( u 1 + 3 d ) 2
= ( u 1 - 8 ) 2 + ( u 1 - 12 ) 2
= 2 ( u 1 - 10 ) 2 + 8 ≥ 8
Vậy u 3 2 + u 4 2 đạt giá trị nhỏ nhất khi u 1 = 10
⇒ u 2019 = - 8062