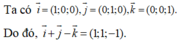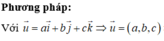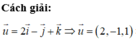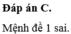Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Muốn chứng tỏ rằng ba vecto u → , v → , w → đồng phẳng ta cần tìm hai số thực p và q sao cho w → = p u → + q v →
Giả sử có w → = p u → + q v →
2 c → – 3 a → = p( a → – 2 b → ) + q(3 b → − c → )
⇔ (3 + p) a → + (3q − 2p) b → − (q + 2) c → = 0 → (1)
Vì ba vecto lấy tùy ý a → , b → , c → nên đẳng thức (1) xảy ra khi và chỉ khi:
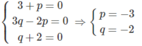
Như vậy ta có: w → = −3 u → − 2 v → nên ba vecto u → , v → , w → đồng phẳng.

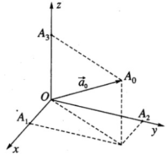
Gọi a 0 → là vecto đơn vị cùng hướng với vecto a →
ta có 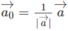
Gọi O A 0 → = a 0 → và các điểm A 1 , A 2 , A 3 theo thứ tự là hình chiếu vuông góc của điểm A 0 trên các trục Ox, Oy, Oz.
Khi đó ta có:
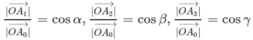
Vì
![]()
![]()
Ta có:
![]()
ta suy ra:
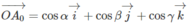
hay
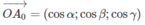
Vì O A 0 → = a 0 → mà | a 0 → | = 1 nên ta có: cos 2 α + cos 2 β + cos 2 γ = 1

Đề bị lỗi công thức kìa bạn. Bạn xem và sửa lại đề dưới post.