Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp: Sử dụng phương pháp loại trừ.
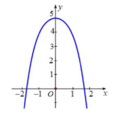
Cách giải: Vì điểm (0;5) thuộc đồ thị hàm số nên ta loại đáp án D.
Vì bề lõm của đồ thị hướng xuống dưới nên dựa vào tính chất của đồ thị hàm số
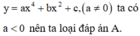
Ta thấy trị tuyệt đối hoành độ giao điểm của đồ thị hình bên nhỏ hơn 2. Nhưng trị tuyệt đối hoành độ giao điểm của đồ thị hàm số ở phương án C là x = 20 4 > 2 . Từ đó loại phương án C.

Đáp án B
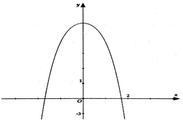
Ta thấy đồ thị hàm số chỉ có một điểm cực trị nên loại đáp án D.
Từ trái sang phải, đồ thị hàm số đi từ dưới lên, do đó hệ số của x 4 phải âm. Suy ra loại được đáp án A.
Với x = ± 2 thì y < 0. Thay x = ± 2 vào hai đáp án B, C ta thấy đáp án B thỏa mãn còn đáp án C không thỏa mãn.

Điều kiện:


Từ đồ thị hàm số y=f(x) ta thấy phương trình f(x)=0 có nghiệm x=-3 (bội 2) và nghiệm đơn x = x 0 ∈ - 1 ; 0 nên ta viết lại f ( x ) = a x + 3 2 x - x 0
Khi đó

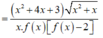
Dựa vào đồ thị ta cũng thấy, đường thẳng y=2 cắt đồ thị hàm số y=f(x) tại ba điểm phân biệt x=-1, x = x 1 ∈ - 3 ; - 1 , x = x 2 < - 3 nên ta viết lại
![]()
Khi đó
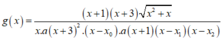
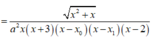
Dễ thấy x = x 0 ∈ - 1 ; 0 nên ta không xét giới hạn của hàm số tại điểm x 0
Ta có:
+) l i m x → 0 + g ( x ) = l i m x → 0 +
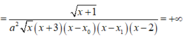
⇒ x = 0 là đường TCĐ của đồ thị hàm số y=g(x)
+) ![]()
⇒ Các đường thẳng x = - 3 , x = x 1 , x = x 2 đều là các đường tiệm cận đứng của đồ thị hàm số y=g(x)
Vậy đồ thị hàm số y=g(x) có tất cả 4 đường tiệm cận đứng.
Chọn đáp án D.
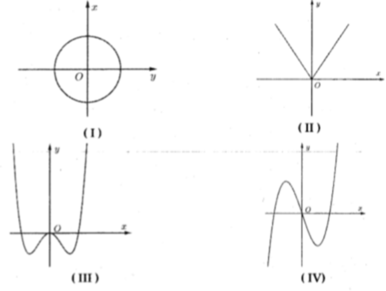
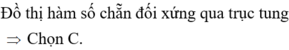

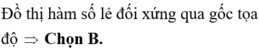
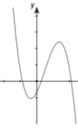

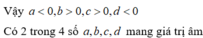
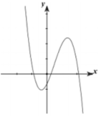

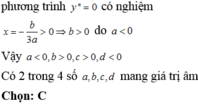



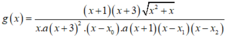



Chọn B.
Từ hình I và II ta thấy tồn tại điểm thuộc trên trục Ox từ đó dựng đường thẳng vuông góc với Ox cắt hai điểm phân biệt trên đồ thị. Mỗi giá trị của x có hai giá trị của y nên hình I và II không phải là hình minh họa đồ thị hàm số