Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Phương trình hoành độ giao điểm của (D1) và (d2) là:
-x+4=x-4
\(\Leftrightarrow-2x=-8\)
hay x=4
Thay x=4 vào (d1), ta được:
y=-4+4=0
Thay x=0 vào (d1), ta được:
\(y=-0+4=4\)
Thay x=0 vào (d2), ta được:
\(y=0-4=-4\)
Vậy: A(0;4); B(0;-4); C(4;0)

a:
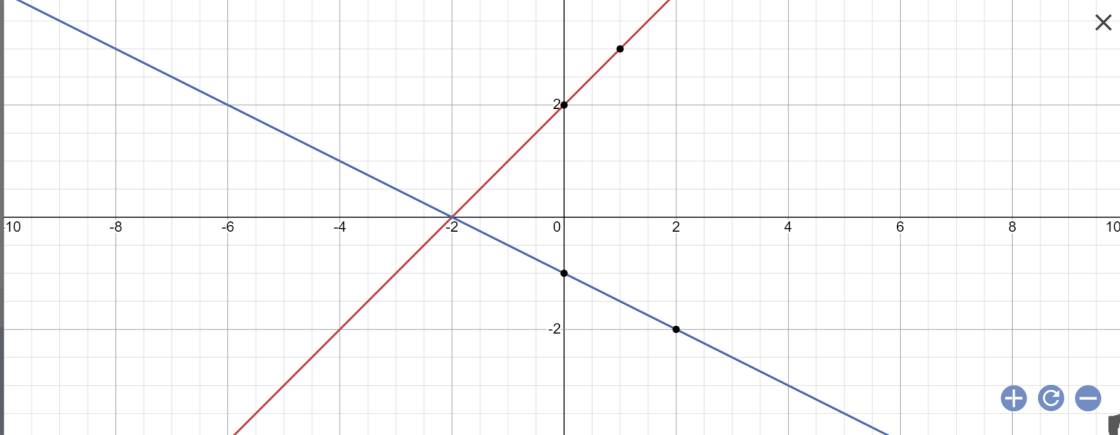
Phương trình hoành độ giao điểm là:
\(x+2=-\dfrac{1}{2}x-1\)
=>\(x+\dfrac{1}{2}x=-1-2\)
=>1,5x=-3
=>x=-3/1,5=-2
Thay x=-2 vào y=x+2, ta được:
y=-2+2=0
Vậy: (d1) cắt (d2) tại điểm A(-2;0) nằm trên trục hoành
b: Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x+2=0+2=2\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{2}x-1=-\dfrac{1}{2}\cdot0-1=-1\end{matrix}\right.\)
A(-2;0); B(0;2); C(0;-1)
\(AB=\sqrt{\left(0+2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(0+2\right)^2+\left(-1-0\right)^2}=\sqrt{2^2+\left(-1\right)^2}=\sqrt{5}\)
\(BC=\sqrt{\left(0-0\right)^2+\left(-1-2\right)^2}=\sqrt{0^2+\left(-3\right)^2}=3\)
Xet ΔABC có \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{\sqrt{5}}{3}\)
nên \(\widehat{B}\simeq48^011'\)
Ta có: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}+48^011'=90^0\)
=>\(\widehat{ACB}=41^049'\)
c: Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=2\sqrt{2}+\sqrt{5}+3\)
Vì ΔABC vuông tại A
nên \(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot2\sqrt{2}\cdot\sqrt{5}=\sqrt{10}\)

a: 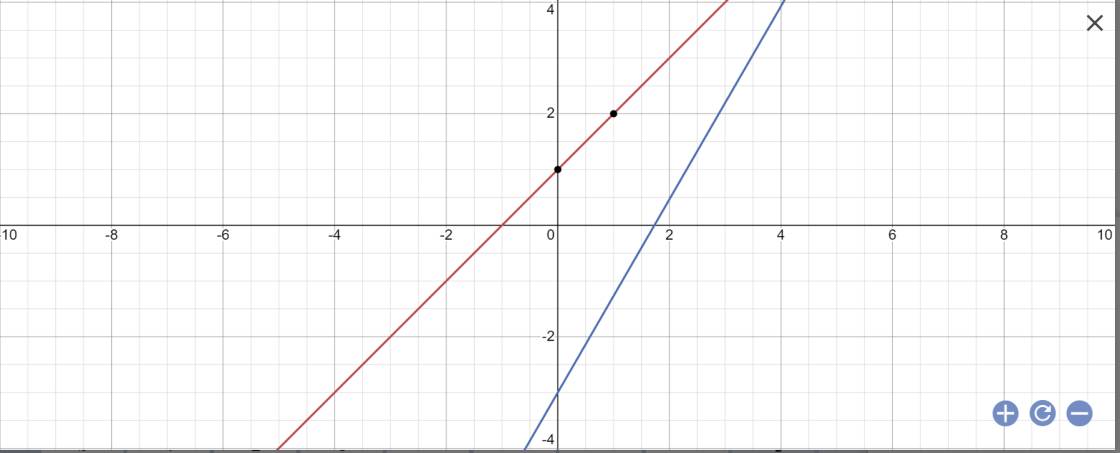
b: Tọa độ A là;
y=0 và x+1=0
=>x=-1 và y=0
Tọa độ B là:
y=0 và x*căn 3-3=0
=>x=căn 3 và y=0
Tọa độ C là:
x+1=xcăn 3-3 và y=x+1
=>\(x=\dfrac{-4}{-\sqrt{3}+1}=2+2\sqrt{3}\) và y=3+3căn 3
A(-1;0); B(căn 3;0); \(C\left(2+2\sqrt{3};3+3\sqrt{3}\right)\)
\(AC=\sqrt{\left(2+2\sqrt{3}+1\right)^2+\left(3\sqrt{3}\right)^2}\simeq8,29\)
\(AB=\sqrt{\left(\sqrt{3}+1\right)^2}\simeq2,73\)
\(BC=\sqrt{\left(2+2\sqrt{3}-\sqrt{3}\right)^2+\left(3+3\sqrt{3}\right)^2}\simeq9,0\left(cm\right)\)
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\simeq-\dfrac{245}{2487}\)
=>góc A=96 độ
\(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}=\dfrac{271}{675}\)
=>góc B=67 độ
=>góc C=17 độ

a: Tọa độ A là:
y=0 và -1/2x+4=0
=>x=8 và y=0
=>A(8;0)
Tọa độ B là;
y=0 và -x+4=0
=>x=4 và y=0
=>B(4;0)
Tọa độ C là;
1/2x+4=-x+4 và y=-x+4
=>x=0 và y=4
=>C(0;4)
b: A(8;0); B(4;0); C(0;4)
\(AB=\sqrt{\left(4-8\right)^2+\left(0-0\right)^2}=4\)
\(AC=\sqrt{\left(0-8\right)^2+\left(4-0\right)^2}=4\sqrt{5}\)
\(BC=\sqrt{4^2+4^2}=4\sqrt{2}\)
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{2}{\sqrt{5}}\)
=>\(sinBAC=\dfrac{1}{\sqrt{5}}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot4\cdot4\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=8\)
\(C=4+4\sqrt{5}+4\sqrt{2}\)

(d1): y = 1/2x + 2
và (d2): y = -x + 2
1. Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ Oxy.
(d1) là đường thẳng đi qua hai điểm (0; 2) và (-4; 0)
(d2) là đường thẳng đi qua hai điểm (0; 2) và (2;0)
2. Tính chu vi và diện tích của tam giác ABC
(d1) và (d2) cùng cắt nhau tại một điểm trên trục tung có tung độ bằng 2
Áp dụng định lý Pi ta go cho các tam giác AOC và BOC vuông ở O ta được:
\(AC=\sqrt{4^2+2^2}=\sqrt{20}=2\sqrt{5}\)
\(BC=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}\)
Chu vi tam giác ABC : AC + BC + AB= 2√5 + 2√2 + 6
≈ 13,30
Diện tích tam giác ABC
\(\frac{1}{2}.OC.AB=\frac{1}{2}.2.6=6CM^2\)
NHÉ THAK NHÌU

a: 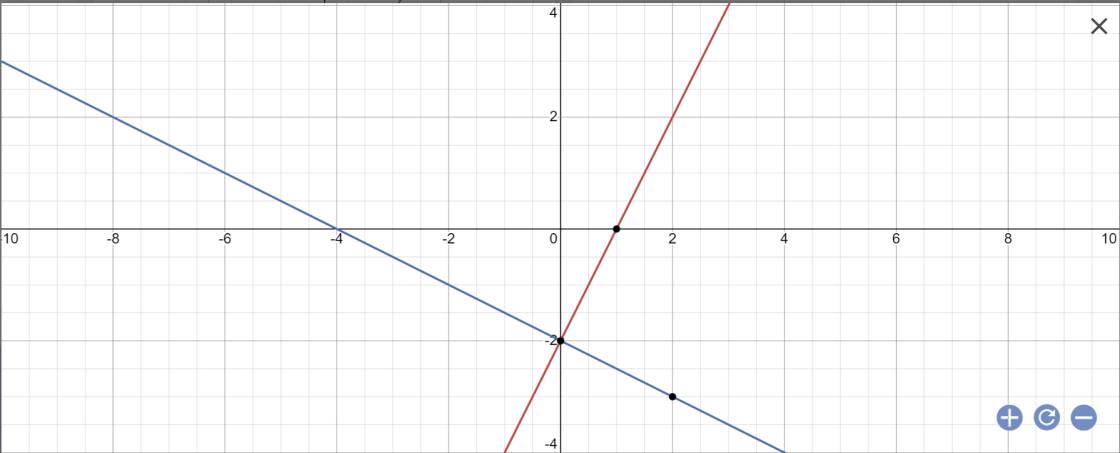
b: Tọa độ A là:
2x-2=-1/2x-2 và y=2x-2
=>x=0 và y=-2
Tọa độ B là:
y=0 và 2x-2=0
=>x=1 và y=0
Tọa độ C là:
y=0 và -1/2x-2=0
=>x=-4; y=0
i: A(0;-2); B(1;0); C(-4;0)
\(\overrightarrow{AB}=\left(1;2\right);\overrightarrow{AC}=\left(-4;2\right)\)
Vì 1*(-4)+2*2=0
nên ΔABC vuông tại A
ii: \(AB=\sqrt{1^2+2^2}=\sqrt{5}\)
\(AC=\sqrt{\left(-4\right)^2+2^2}=2\sqrt{5}\)
\(BC=\sqrt{5+20}=5\left(cm\right)\)
\(C_{ABC}=AB+AC+BC=5+3\sqrt{5}\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot2\sqrt{5}\cdot\sqrt{5}=5\left(cm^2\right)\)

a, HS Tự làm
b, Tìm được C(–2; –3) là tọa độ giao điểm của d 1 và d 2
c, Kẻ OH ⊥ AB (CH ⊥ Ox)
S A B C = 1 2 C H . A B = 9 4 (đvdt)

1) \(\left\{{}\begin{matrix}\left(d_1\right):y=2x\\\left(d_2\right):y=-\dfrac{1}{2}x+5\end{matrix}\right.\)
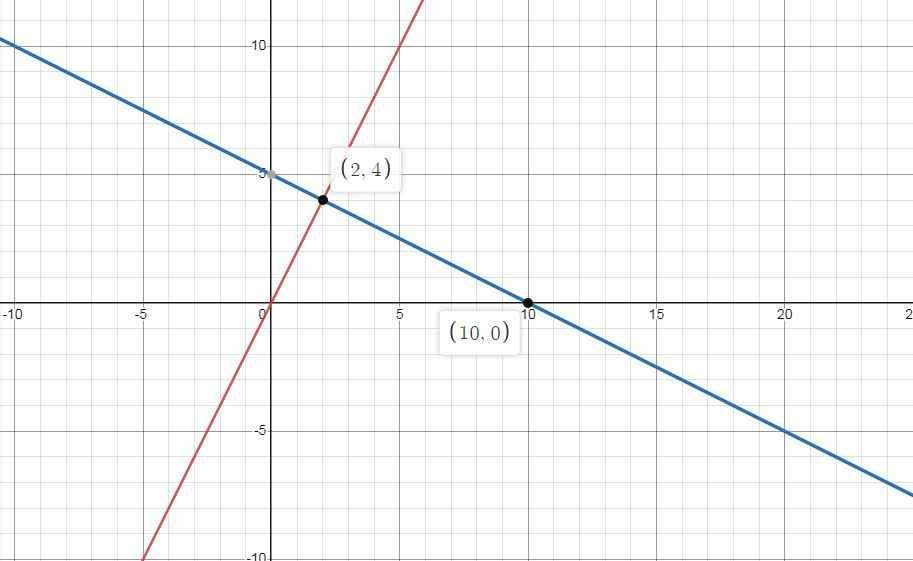
2) Theo đồ thi ta có :
\(\left(d_1\right)\cap\left(d_2\right)=A\left(2;4\right)\)
3) \(\left(d_2\right)\cap Ox=B\left(a;0\right)\)
\(\Leftrightarrow-\dfrac{1}{2}a+5=0\)
\(\Leftrightarrow\dfrac{1}{2}a=5\)
\(\Leftrightarrow a=10\)
\(\Rightarrow\left(d_2\right)\cap Ox=B\left(10;0\right)\)
4) \(OA=\sqrt[]{\left(2-0\right)^2+\left(4-0\right)^2}=\sqrt[]{20}=2\sqrt[]{5}\)
\(OB=\sqrt[]{\left(10-0\right)^2+\left(0-0\right)^2}=\sqrt[]{10^2}=10\)
\(AB=\sqrt[]{\left(10-2\right)^2+\left(0-4\right)^2}=\sqrt[]{80}=4\sqrt[]{5}\)
Ta thấy :
\(OA^2+AB^2=20+80=OB^2=100\)
\(\Rightarrow\Delta OAB\) vuông tại A
\(\Rightarrow\widehat{OAB}=90^o\)
\(sin\widehat{AOB}=\dfrac{AB}{OB}=\dfrac{4\sqrt[]{5}}{10}=\dfrac{2\sqrt[]{5}}{5}\)
\(\Rightarrow\widehat{AOB}\sim63,43^o\)
\(\Rightarrow\widehat{OBA}=90^o-63,43^o=26,57^o\)
5) Chu vi \(\Delta OAB\) :
\(AB+OA+OB=4\sqrt[]{5}+2\sqrt[]{5}+10=10\sqrt[]{5}+10=10\left(\sqrt[]{5}+1\right)\left(đvmd\right)\)
Diện tích \(\Delta OAB\) :
\(\dfrac{1}{2}AB.OA=\dfrac{1}{2}.4\sqrt[]{5}.2\sqrt[]{5}=20\left(đvdt\right)\)