Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: S=A-B
\(=\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-1-\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{2x+1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)

\(M=\left(\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}-1}\right):\left(\sqrt{x}+\dfrac{\sqrt{x}}{\sqrt{x}-1}\right)\) với x>0;x≠1
\(=\left(\dfrac{x\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(x-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{x-\sqrt{x}+\sqrt{x}}{\sqrt{x}-1}\)
\(M=\dfrac{x\sqrt{x}+1-x\sqrt{x}-x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}-1}{x}=\dfrac{-x+\sqrt{x}+2}{x\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(2-\sqrt{x}\right)}{x\left(\sqrt{x}+1\right)}=\dfrac{2-\sqrt{x}}{x}\)
vậy M=\(\dfrac{2-\sqrt{x}}{x}\)
vì x>0 nên để \(M< 0\Leftrightarrow\dfrac{2-\sqrt{x}}{x}< 0\Leftrightarrow2-\sqrt{x}< 0\Leftrightarrow\sqrt{x}>2\Leftrightarrow x>4\)

Ta có: M=A+B
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{11\sqrt{x}-3}{x-9}\)
\(=\dfrac{2x-6\sqrt{x}+x+4\sqrt{x}+3+11\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)

a) \(P=\dfrac{1}{2-\sqrt{3}}+\dfrac{1}{2+\sqrt{3}}\)
\(=\dfrac{2+\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}+\dfrac{2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\dfrac{2+\sqrt{3}+2-\sqrt{3}}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=\dfrac{4}{4-3}\)
\(=4\)
b) \(Q=\left(1+\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\right).\dfrac{1}{\sqrt{x}}vớix>0,x\ne4\)
\(=\left(\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\sqrt{x}-2}\right).\dfrac{1}{\sqrt{x}}\)
\(=\)\(\dfrac{2\sqrt{x}}{\sqrt{x}-2}.\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2}{\sqrt{x}-2}\)

\(a,P=\dfrac{\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{2-\sqrt{x}}{\sqrt{x}}=\dfrac{-2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}=\dfrac{-2}{\sqrt{x}+2}\\ P=-\dfrac{3}{5}\Leftrightarrow\dfrac{2}{\sqrt{x}+2}=\dfrac{3}{5}\\ \Leftrightarrow3\sqrt{x}+6=10\Leftrightarrow\sqrt{x}=\dfrac{4}{3}\Leftrightarrow x=\dfrac{16}{9}\left(tm\right)\)
\(P=-\dfrac{3}{5}\) sao suy ra đc \(\dfrac{2}{\sqrt{x}+2}=\dfrac{3}{5}\) thế

Bài 1:
a: \(B=\dfrac{\sqrt{x}+x+\sqrt{x}-x}{1-x}\cdot\dfrac{x-1}{3-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}-3}\)
b: Để B=-1 thì \(2\sqrt{x}=-\sqrt{x}+3\)
=>3 căn x=3
=>căn x=1
hay x=1(loại)

a: \(A=\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{1}{x-\sqrt{x}}\right)\cdot\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}-1}\)
\(=\dfrac{x-\sqrt{x}-\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}-1}\)
\(=\dfrac{x-2\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)^2}\)
b: Để A<=3/căn x thì \(\dfrac{x-2\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)^2}< =\dfrac{3}{\sqrt{x}}\)
=>\(\dfrac{x-2\sqrt{x}-1-3x+6\sqrt{x}-3}{\left(\sqrt{x}-1\right)^2}< =0\)
=>\(-2x+4\sqrt{x}-4< =0\)
=>\(x-2\sqrt{x}+2>=0\)(luôn đúng)

Câu 2:
a,
diện tích nhựa là: 2π. (0,4:2). 16= 6,4π (cm2)
b,
gọi chữ số hàng chục là a (a>0, a ∈N)
hàng đơn vị là b (b∈N)
hiệu 2 chữ số là: a-b=3 (1)
tổng bình phương 2 chữ số là: a2+b2=45 (2)
từ (1) và (2) ta có hpt:
\(\left\{{}\begin{matrix}a-b=3\\a^2+b^2=45\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}a=6\\b=3\end{matrix}\right.\)
vậy chữ số đó là 63
Câu 1
a, Thay x=25 vào biểu thức B ta có
B=\(\dfrac{\sqrt{25}-3}{\sqrt{25}-1}=\dfrac{5-3}{5-1}=\dfrac{2}{4}=\dfrac{1}{2}\)
b, Ta có M=\(A\cdot B\)
⇒\(\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}\right)\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)
=\(\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)
=\(\dfrac{3x-3\sqrt{x}}{\left(\sqrt{x}+3\right)}\cdot\dfrac{1}{\sqrt{x}-1}\)
=\(\dfrac{3\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
=\(\dfrac{3\sqrt{x}}{\sqrt{x}+3}\)
c, Để M<\(\sqrt{M}\)
Thì\(\text{}\text{}\text{}\text{}\dfrac{3\sqrt{x}}{\sqrt{x}+3}< \sqrt{\dfrac{3\sqrt{x}}{\sqrt{x}+3}}\)
⇔\(\text{}\text{}\text{}\text{}\dfrac{3\sqrt{x}}{\sqrt{x}+3}< \dfrac{\sqrt{3\sqrt{x}\left(\sqrt{x}+3\right)}}{\sqrt{x}+3}\)
⇔\(\text{}\text{}\text{}\text{}3\sqrt{x}< \sqrt{3\sqrt{x}\left(\sqrt{x}+3\right)}\)
⇔\(\text{}\text{}\text{}\text{}9x< 3\sqrt{x}\left(\sqrt{x}+3\right)\)
⇔\(\text{}\text{}\text{}\text{}3\sqrt{x}< \sqrt{x}+3\)
⇔\(\text{}\text{}\text{}\text{}2\sqrt{x}< 3\)
⇔\(\text{}\text{}\text{}\text{}\sqrt{x}< \dfrac{3}{2}\)
⇒\(\left\{{}\begin{matrix}x\ge0\\x< \dfrac{9}{4}\end{matrix}\right.\)
⇒\(0\le x< \dfrac{9}{4}\)

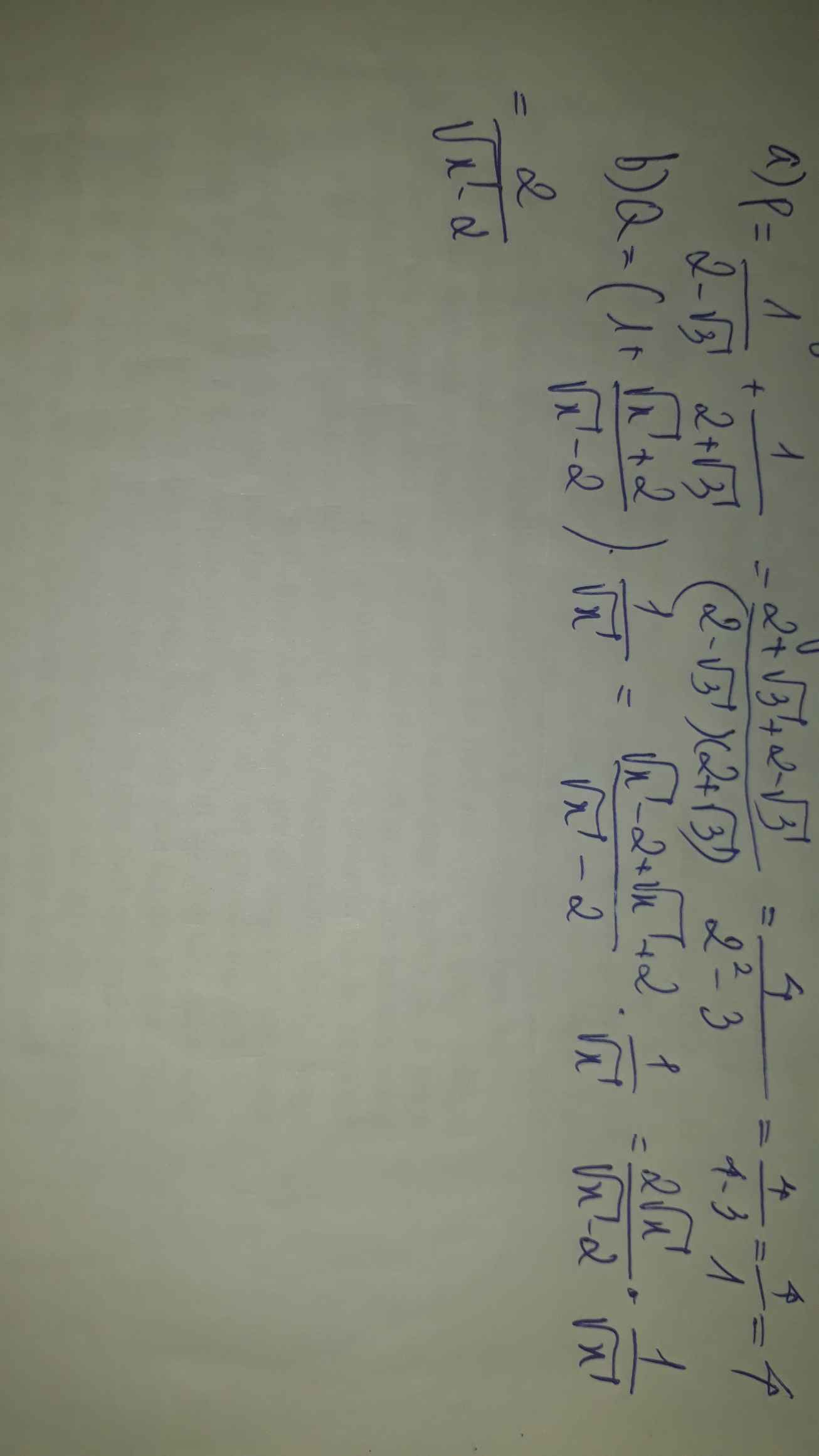

Ta có: M=A+B
\(=\dfrac{x-\sqrt[3]{x}}{x-1}+\dfrac{1}{\sqrt[3]{x}-1}+\dfrac{1}{\sqrt[3]{x^2}+\sqrt[3]{x}+1}\)
\(=\dfrac{x-\sqrt[3]{x}}{\left(\sqrt[3]{x}-1\right)\left(\sqrt[3]{x^2}+\sqrt[3]{x}+1\right)}+\dfrac{\sqrt[3]{x^2}+\sqrt[3]{x}+1+\sqrt[3]{x}-1}{\left(\sqrt[3]{x}-1\right)\left(\sqrt[3]{x^2}+\sqrt[3]{x}+1\right)}\)
\(=\dfrac{x+\sqrt[3]{x}+\sqrt[3]{x^2}}{\left(\sqrt[3]{x}-1\right)\left(\sqrt[3]{x^2}+\sqrt[3]{x}+1\right)}\)
\(=\dfrac{\sqrt[3]{x}}{\sqrt[3]{x}-1}\)