
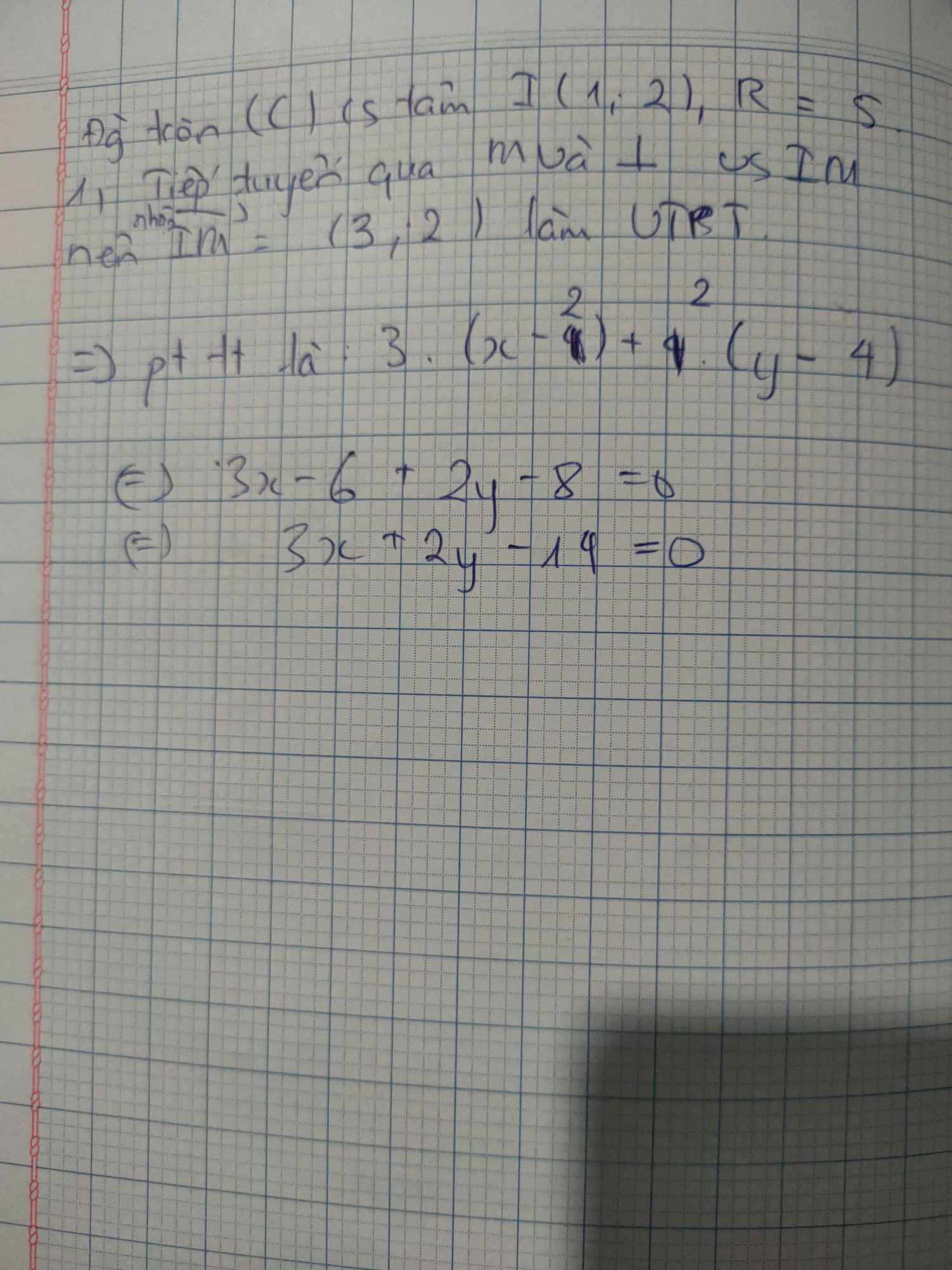
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

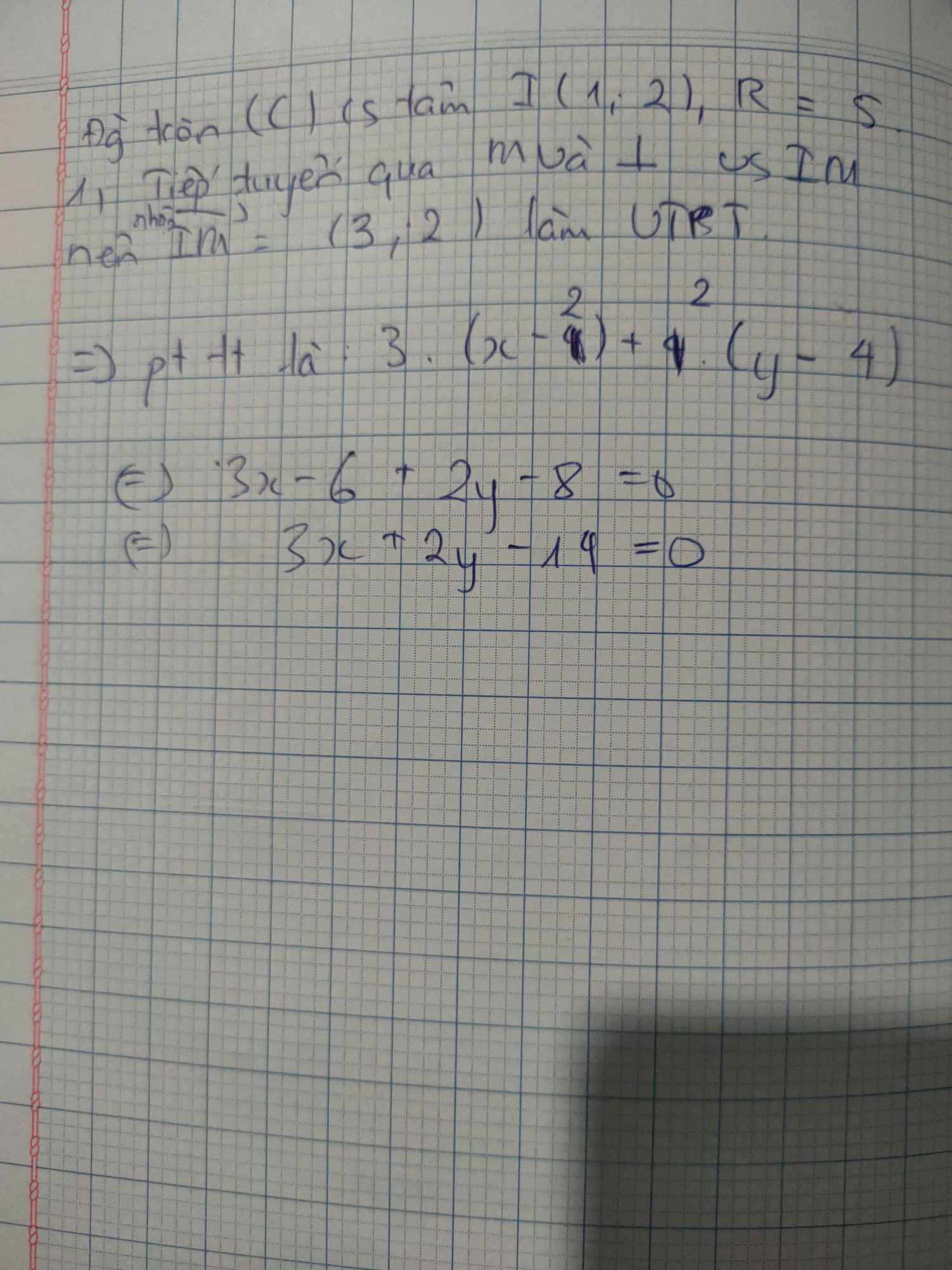

Câu 1:
\(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-sin^2x=1-\left(\frac{4}{5}\right)^2=\frac{9}{15}\)
\(\Leftrightarrow cos^2x=\frac{\pm3}{5}\).
Câu 2:
Đường tròn \(\left(C\right)\)có tâm \(I\left(2,-1\right)\)bán kính \(R=\sqrt{25}=5\).
Gọi \(d\)là tiếp tuyến của đường tròn \(\left(C\right)\)tại điểm \(M\). Khi đó \(IM\)và \(d\)vuông góc với nhau.
\(\Rightarrow\overrightarrow{IM}=\left(3,4\right)\)là một vector pháp tuyến của \(d\)
Suy ra phương trình \(d:3\left(x-5\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-27=0\).

\(\left(C\right):\left(x-2\right)^2+\left(y-1\right)^2=25\)
\(\Rightarrow\left(C\right)\) có tâm \(I\left(2;1\right)\) ; Bán kính \(R=5\)
\( \left(C\right)//d:5x-12y+67=0\)
nên \(\Delta:5x-12y+m=0\left(m\ne67\right)\)
Vì \(d\) có \(VTPT\overrightarrow{n}=\left(5;-12\right)\) cũng là \(VTPT\) của \(\Delta\)
\(R=d\left(I,\Delta\right)=\dfrac{\left|5x_I-12y_I+m\right|}{\sqrt{5^2+\left(-12\right)^2}}\Leftrightarrow\dfrac{\left|5.2-12.1+m\right|}{13}=5\)
\(\Leftrightarrow\left|-2+m\right|=65\)
\(\Leftrightarrow\left[{}\begin{matrix}-2+m=65\\-2+m=-65\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=67\left(ktm\right)\\m=-63\left(tm\right)\end{matrix}\right.\)
Vậy pt tiếp tuyến là \(5x-12y-63=0\)
(x-2)^2+(y-1)^2=25
=>R=5; I(2;1)
(d')//(d) nên (d'): 5x-12y+c=0
Theo đề, ta có; d(I;(d'))=5
=>\(\dfrac{\left|5\cdot2+\left(-12\right)\cdot1+c\right|}{\sqrt{5^2+12^2}}=5\)
=>|c-2|=65
=>c=67 hoặc c=-63

a) Để tìm phương trình đường tròn © có tâm I(2,3) đi qua điểm A(5,7), ta sử dụng công thức khoảng cách từ điểm đến tâm đường tròn:
$I\hat{A} = \sqrt{(x_A - x_I)^2 + (y_A - y_I)^2}$
Với I là tâm đường tròn, A là điểm trên đường tròn.
Ta có: $x_I = 2$, $y_I = 3$, $x_A = 5$, $y_A = 7$
Thay vào công thức ta được:
$\sqrt{(5-2)^2 + (7-3)^2} = \sqrt{34}$
Vậy bán kính của đường tròn là $\sqrt{34}$.
Phương trình đường tròn © có tâm I(2,3) và bán kính $\sqrt{34}$ là:
$(x-2)^2 + (y-3)^2 = 34$
b) Để tìm phương trình tiếp tuyến của đường tròn © : $(x-1)^2 + ( y+5)^2 =4$, ta cần tìm đạo hàm của phương trình đường tròn tại điểm cần tìm tiếp tuyến.
Ta có phương trình đường tròn chính giữa:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Tại điểm M(x,y) trên đường tròn, ta có:
$(x-1)^2 + (y+5)^2 = 2^2$
Đạo hàm hai vế theo x:
$2(x-1) + 2(y+5)y' = 0$
Suy ra:
$y' = -\frac{x-1}{y+5}$
Vậy tại điểm M(x,y), phương trình tiếp tuyến của đường tròn là:
$y - y_M = y'(x-x_M)$
Thay $y'$ bằng $\frac{-(x-1)}{y+5}$ và $x_M$, $y_M$ bằng 1, -5 ta được:
$y + 5 = \frac{-(x-1)}{y+5}(x-1)$
Simplifying:
$x(y+5) + y(x-1) = 6$
Đường thẳng (d) có phương trình là $3x + 4y - 1 = 0$. Vì tiếp tuyến song song với đường thẳng (d) nên hệ số góc của tiếp tuyến

a) Thay điểm \(M(4;6)\)vào phương trình đường tròn \({x^2} + {y^2} - 2x - 4y - 20 = 0\)
ta có:
\({4^2} + {6^2} - 2.4 - 4.6 - 20 = 0\)
Suy ra, điểm M thuộc đường tròn (C)
b) Đường tròn có tâm \(I(1;2)\)
Phương trình tiếp tuyến d của (C) tại \(M(4;6)\) là:
\(\begin{array}{l}\left( {1 - 4} \right)\left( {x - 4} \right) + \left( {2 - 6} \right)\left( {y - 6} \right) = 0\\ \Leftrightarrow 3x + 4y -36 = 0\end{array}\)
c) Tiếp tuyến của đường tròn song song với đường thẳng \(4x + 3y + 2022 = 0\) nên phương trình có dạng \(d:4x + 3y + c = 0\)
Ta có tâm và bán kính của đường tròn là: \(I(1;2),r = \sqrt {{1^2} + {2^2} + 20} = 5\)
Khoảng cách từ tâm đến tiếp tuyến là bán kính nên: \(d\left( {I,d} \right) = \frac{{\left| {4.1 + 3.2 + c} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 5 \Rightarrow \left[ \begin{array}{l}c = 15\\c = - 35\end{array} \right.\)
Vậy đường tròn (C) có hai tiếp tuyến song song với đường thẳng \(4x + 3y + 2022 = 0\) là \({d_1}:4x + 3y + 15 = 0,{d_2}:4x + 3y - 35 = 0\)

a) Ta có \(I\left( {2; - 3} \right)\) và \(R = \sqrt {{2^2} + {{\left( { - 3} \right)}^2} - \left( { - 12} \right)} = 5\)
b) Ta có: \({5^2} + {1^2} - 4.5 + 6.1 - 12 = 0\). Suy ra M thuộc \(\left( C \right)\). Tiếp tuyến d của (C) tại M có vectơ pháp tuyến là \(\overrightarrow {{n_d}} = \overrightarrow {IM} = \left( {3;4} \right)\), đồng thời d đi qua điểm \(M\left( {5;1} \right)\).
Vậy phương trình của d là \(3\left( {x - 5} \right) + 4\left( {y - 1} \right) = 0 \Leftrightarrow 3x + 4y - 19 = 0\).

\(PT\left(C\right):\left(x+1\right)^2+\left(y-7\right)^2=85\)
\(\Rightarrow\) Tâm \(I\left(-1;7\right)\) và bán kính là \(\sqrt{85}\)
PT tiếp tuyến qua \(M\left(1;-2\right)\Rightarrow x_0=1,y_0=-2\)
\(PT\) tiếp tuyến có dạng \(\left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0\)
\(\Leftrightarrow\left(-1-1\right)\left(x-1\right)+\left(7+2\right)\left(y+2\right)=0\)
\(\Leftrightarrow-2\left(x-1\right)+9\left(y+2\right)=0\)
\(\Leftrightarrow-2x+2+9y+18=0\)
\(\Leftrightarrow-2x+9y+20=0\)