Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

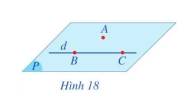
a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d
b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d

Chọn B
Đáp án A sai do đường thẳng a có thể nằm trong mặt phẳng (EFG).
Đáp án C sai do mặt phẳng (ABC) có thể trùng với mặt phẳng (EFG).
Đáp án D sai do mặt phẳng (ABC) có thể trùng với mặt phẳng (EFG).

Nhận xét: học sinh có thể nhầm cho rằng mỗi tam giác là một chỉnh hợp chập 3 của 18, nên số tam giác là A183 (phương án A); hoặc suy luận một tam giác có 3 đỉnh nên 18 điểm cho ta 18/3 = 6 tam giác (phương án C); hoặc suy luận 18 điểm có 18! Cách và mỗi tam giác có 3 đỉnh nên số tam giác là 18!/3 cách (phương án D)
- Do ![]()
nên mỗi vecto là một chỉnh hợp chập hai của 18.
Vì vậy, số vecto là A182 (chọn đáp án là A)

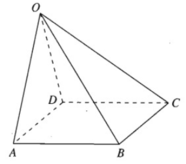
Giả sử bốn điểm A, B, C, D tạo thành một hình bình hành ta có:
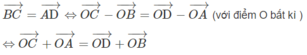
Ngược lại, giả sử ta có hệ thức:
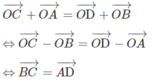
Vì A, B, C, D không thẳng hàng nên tứ giác ABCD là hình bình hành.

Cứ chọn 3 điểm không thẳng hàng bất kì ta được một tam giác.
Việc lập các tam giác chính là chọn 3 điểm trong tập hợp 6 điểm đã cho và chính là tổ hợp chập 3 của 6.
Vậy có:
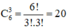 cách lập.
cách lập.

Chọn A
Ta chọn bất kì 3 điểm trong 18 điểm đã cho thì tạo thành một tam giác.
Do đó số tam giác được tạo thành là số cách chọn 3 điểm phân biệt bất kỳ (không kể thứ tự) từ 18 điểm đã cho.
Vậy có tất C 18 3 tam giác.

Đáp án là B
Cứ 3 điểm phân biệt không thẳng hàng tạo thành một tam giác.
Lấy 3 điểm bất kỳ trong 6 điểm phân biệt thì số tam giác cần tìm chính là một tổ hợp chập 3 của 6 phần tử (điểm).
Như vậy, ta có C 6 3 = 20 tam giác.

Đáp án D
Với 2 điểm bất kỳ luôn tạo thành 2 vectơ.
Số vectơ được tạo thành: ![]() vectơ.
vectơ.

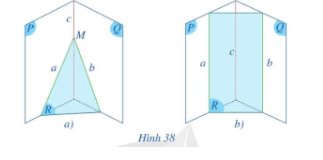
– Ta có: a ∩ b = {M}
Mà a ⊂ (P); b ⊂ (Q)
Nên M ∈ (P) và M ∈ (Q)
Do đó M là giao điểm của (P) và (Q).
Mà (P) ∩ (Q) = c, suy ra M ∈ c.
Vậy đường thằng c đi qua điểm M.
– Giả sử trong mặt phẳng (P) có a ∩ c = {N}.
Khi đó N ∈ a mà a ⊂ (R) nên N ∈ (R)
N ∈ c mà c ⊂ (Q) nên N ∈ (Q)
Do đó N là giao điểm của (R) và (Q).
Mà (Q) ∩ (R) = b
Có \(C^2_4=6\left(đường\right)\) đi qua 2 điểm trong 4 điểm đã cho