Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta chứng minh được BEDF là hình bình hành Þ BE = DF và E B F ^ = C D F ^ .
Cách khác: DAEB = DCFD (c.g.c) suy ra BE = DF và A B E ^ = C D F ^ .

b) Vì BEDF hình bình hành Þ ĐPCM

Xét tứ giác BEDF có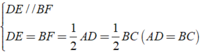
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên
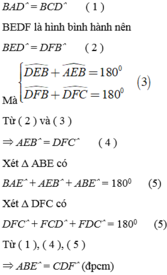

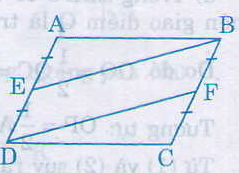
a/ Do ABCD là hình bình hành nên:
- AB=CD; AD=BC
- Mà E là trung điểm của AD, F là trung điểm của BC
=> AE=ED=BF=FC
Xét △ABE và △FCD có:
- AE=CF (cmt)
- Góc BAE = Góc FCD (gt)
- AB=CD (gt)
=> △ABE=△CDF (c.g.c)
Vậy: BE=DF; góc ABE = góc CDF (đpcm)
b/ Ta có:
- BC // AD (gt)
- Tia BF thuộc tia BC, tia DE thuộc tia AD
=> BF // DE
DE = BF (cmt)
=> DEBF là hình bình hành (Tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành)
Vậy: EB // DF (đpcm)

Bài giải:
Tứ giác BEDF có:
DE // BF ( vì AD // BC)
DE = BF \(\left(DE=\dfrac{1}{2}AD=\dfrac{1}{2}BC=BF\right)\)
Nên BEDF là hình bình hành.
Suy ra BE = DF.
A B D C E F ) ( x x = = = =
Xét \(\Delta ABF\) và \(\Delta CDE\) có :
\(AB=CD\left(gt\right)\)
Góc \(A\) \(=\) Góc \(B\) \((gt)\)
\(AE=CF\left(=\dfrac{1}{2}AD=\dfrac{1}{2}BC\right)\)
Vậy \(\Delta ABE=\Delta CDF\left(c.g.c\right)\)
\(\Rightarrow BE=DF\) (2 cạnh tương ứng)
P/s : Đây là lần đầu em vẽ hình trên máy nên dễ sai sót ạ,với lại em khong thấy kí hiệu góc ở đâu ạ :v Thông cảm cho em
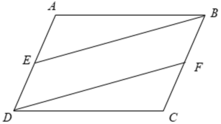
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

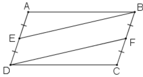
Cách 1:
+ ABCD là hình bình hành ⇒ AB = CD, AD = BC, Â = Ĉ.
+ E là trung điểm của AD ⇒ AE = AD/2
F là trung điểm của BC ⇒ CF = BC/2
Mà AD = BC (cmt) ⇒ AE = CF.
+ Xét ΔAEB và ΔCFD có: AB = CD, Â = Ĉ, AE = CF (cmt)
⇒ ΔAEB = ΔCFD (c.g.c)
⇒ EB = DF.
Cách 2:
ABCD là hình bình hành ⇒ AD//BC và AD = BC.
+ AD // BC ⇒ DE // BF
+ E là trung điểm của AD ⇒ DE = AD/2
F là trung điểm của BC ⇒ BF = BC/2
Mà AD = BC ⇒ DE = BF.
+ Tứ giác BEDF có:
DE // BF và DE = BF
⇒ BEDF là hình bình hành
⇒ BE = DF.