Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

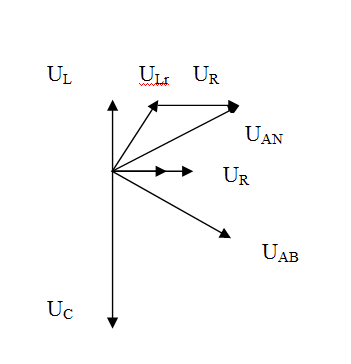
Ta có: \(U_{AB}=U_{AN}=\sqrt{3}U_{MN}=120V\) \(U_R=120V\) \(U_{AB}=U_{AN}\) do đó \(Z_L=U_{LC}\) hay góc hợp giữa \(U_{AB}\) và I bằng góc hợp bởi \(U_{AN}\) và I (cùng có R và r) Mặt khác theo đầu bài của các góc bằng nhau ta suy ra được \(\overrightarrow{U_{AN}}\) là phân giác của góc hợp bởi \(U_{Lr}\) và I \(\overrightarrow{U_{AN}}=\overrightarrow{U_{Lr}}+\overrightarrow{U_R}\) Xét tam giác đã tịnh tiến \(\overrightarrow{U_R}\) lên trên thì theo góc so le của 2 đường song song suy ra đây là tam giác cân \(U_{Lr}=U_R=120V\) Từ đó suy ra góc nhỏ trong tam giác bằng \(\pi\text{ /}6\) Do đó \(U_L=60\sqrt{3}V\) \(Z_L=\frac{U_L}{I}=15\sqrt{6}\Omega\)
|

Bạn vẽ giản đồ véc tơ sẽ suy ra đc \(Z_d=30\Omega\)
\(\Rightarrow r=Z_d\cos 60^0=15\Omega\)
Vậy điện trở hoạt động của mạch
\(R+r=45\Omega\)

\(Z_L=\omega L=100\Omega\)
Ta áp dụng một tính chất của mạch RLC khi C thay đổi để Uc max là lúc đó u mạch vuông pha với uRL.
Như vậy, bài này theo giả thiết uAB lệch pha pi/2 so với uAM là thỏa mãn điều kiện trên.
=> \(Z_C=\frac{R^2+Z_L^2}{Z_L}=\frac{50^2+100^2}{100}=125\Omega\)
=> C

Giải thích: Đáp án C
+ Cường độ dòng điện trong mạch sớm pha π 4 so với điện áp u nên:
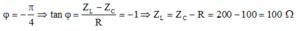
+ Giá trị của L là: 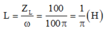

\(Z_L=40\Omega\)
\(U_L=IZ_L=\frac{U}{Z}Z_L=\frac{120.40}{\sqrt{30^2+\left(40-Z_C\right)^2}}\)
Suy ra \(U_L\)max khi \(Z_C=40\Omega\)
\(U_{Lmax}=\frac{120.40}{30}=160V\)

Vì đề bài không nói i sớm pha hay trễ pha với u, nên ta tìm \(\cos\varphi\)
\(\cos\varphi=\frac{R}{\sqrt{R^2+Z_C^2}}=\cos\frac{\pi}{3}=\frac{1}{2}\)
\(\Rightarrow R^2+Z_C^2=4R^2\Rightarrow Z_C=\sqrt{3}.R=100\sqrt{3}\Omega\)
\(\Rightarrow\omega=\frac{1}{Z_C.C}=\frac{1}{100\sqrt{3}.\frac{10^{-3}}{12\sqrt{3}\pi}}=120\pi\)
\(\Rightarrow f=60Hz\)

\(I=10\sqrt{2}sin100\pi t\) trong đó \(\omega=100\pi\)(rad/s)
Ta có: \(Z_C=\dfrac{1}{\omega C}=\dfrac{1}{100\pi\cdot\dfrac{250}{\pi}}=4\cdot10^{-5}\Omega\)
\(U_0=I_0\cdot Z_C=10\sqrt{2}\cdot4\cdot10^{-5}=4\sqrt{2}\cdot10^{-4}V\)
Ta có pha=\(\dfrac{\pi}{2}\) nên:
\(U=U_0cos\left(\omega t+\varphi\right)=4\sqrt{2}\cdot10^{-4}\cdot cos\left(100\pi t-\dfrac{\pi}{2}\right)\)