Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: \(x=\sqrt{28-16\sqrt{3}}+2\sqrt{3}\)
\(=4-2\sqrt{3}+2\sqrt{3}\)
=4
Thay x=4 vào B, ta được:
\(B=\dfrac{2-4}{2}=-1\)

Lời giải:
a.
\(A=\frac{(x\sqrt{x}-4x)-(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{x}-2)(\sqrt{x}-1)}\)
ĐKXĐ: \(\left\{\begin{matrix} x\geq 0\\ \sqrt{x}-4\neq 0\\ \sqrt{x}-2\neq 0\\ \sqrt{x}-1\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 0\\ x\neq 16\\ x\neq 4\\ x\neq 1\end{matrix}\right.\)
\(A=\frac{x(\sqrt{x}-4)-(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{2}-2)(\sqrt{x}-1)}=\frac{(x-1)(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{x}-2)(\sqrt{x}-1)}\)
\(=\frac{(\sqrt{x}-1)(\sqrt{x}+1)(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{x}-2)(\sqrt{x}-1)}=\frac{\sqrt{x}+1}{2(\sqrt{x}-2)}\)
b.
Với $x$ nguyên, để $A\in\mathbb{Z}$ thì $\sqrt{x}+1\vdots 2(\sqrt{x}-2)}$
$\Rightarrow \sqrt{x}+1\vdots \sqrt{x}-2$
$\Leftrightarrow \sqrt{x}-2+3\vdots \sqrt{x}-2$
$\Leftrightarrow 3\vdots \sqrt{x}-2$
$\Rightarrow \sqrt{x}-2\in\left\{\pm 1;\pm 3\right\}$
$\Rightarrow x\in\left\{1;9;25\right\}$
Thử lại thấy đều thỏa mãn.

a: \(A=\dfrac{x\left(\sqrt{x}-4\right)-\left(\sqrt{x}-4\right)}{2x\sqrt{x}-8x-6x+24\sqrt{x}+4\sqrt{x}-16}\)
\(=\dfrac{\left(\sqrt{x}-4\right)\left(x-1\right)}{\left(\sqrt{x}-4\right)\left(2x-6\sqrt{x}+4\right)}=\dfrac{x-1}{2x-6\sqrt{x}+4}\)
\(=\dfrac{x-1}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{2\sqrt{x}-4}\)
b: Để A nguyên thì \(2\sqrt{x}+2⋮2\sqrt{x}-4\)
\(\Leftrightarrow2\sqrt{x}-4\in\left\{2;-2;6\right\}\)
hay \(x\in\left\{9;1;25\right\}\)

a) Rút gọn:
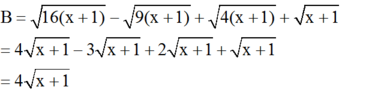
b) Để B = 16 thì:
![]()
⇔ x + 1 = 16 ⇔ x = 15 (thỏa mãn x ≥ -1)
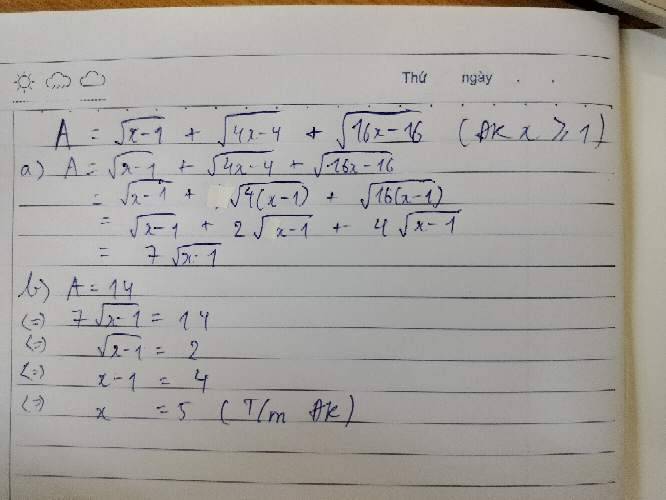
Đề phải như này không bạn?
a) \(B=\sqrt{x^2-4x+4}-\sqrt{x^2+4x+4}\)
\(\Leftrightarrow B=\sqrt{\left(x-2\right)^2}-\sqrt{\left(x+2\right)^2}\)
\(\Leftrightarrow B=\left|x-2\right|-\left|x+2\right|\)
b) Thay B=-2 ta có |x-2|-|x+2|=-2
TH1: x-2-(x+2)=2
<=> x-2-x-2=2
<=> -4=2 (vô lí)
TH2: x-2+x+2=2
<=> 2x=2
<=> x=1 (thõa mãn)
TH3: -(x-2)-(x+2)=2
<=> -x-2-x-2=2
<=> -2x-4=2
<=> -2x=6
<=> x=-3 (TM)
TH4: -(x-2)+x+2=2
<=> -x-2+x+2=2
<=> 0=2 (vô lí)
Vậy x=-3 hoặc x=1 thì B=-2