Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

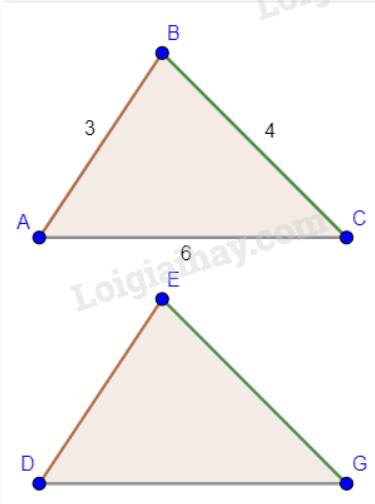
\(\Delta ABC = \Delta DEG\) nên AB = DE, BC = EG, CA = GD.
Vậy độ dài các cạnh của tam giác DEG lần lượt là: \(DE = 3\)cm,\(EG = 4\)cm,\(GD = 6\)cm.

b) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
Suy ra: BA=BE(hai cạnh tương ứng)
hay ΔBAE cân tại B
c) Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(ΔABD=ΔEBD)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: DF=DC(hai cạnh tương ứng)
mà DE<DC(ΔDEC vuông tại E)
nên DE<DF

a)Áp dụng định lí pytago vào tam giác ABC vuông tại A, ta có
BC^2=AB^2+AC^2
=>BC^2=4^2+3^2
=>BC^2=16+9=25
=>BC=căn25=5 (cm)
vậy,BC=5cm
b)Xét tam giác ABC và AED có
AB=AE(gt)
 là góc chung
AC=AD(gt)
=>tam giác ABC=tam giác AED(c-g-c)
Xét tam giác AEB có:Â=90*;AE=AB
=>tam giác AEB vuông cân tại A
Vậy tam giác AEB vuông cân
c)Ta có EÂM+BÂM=90*
mà BÂM+MÂB=90*
=>EÂM=MÂB
mà MÂB=AÊD(cm câu b)
=>EÂM=AÊD hay EÂM=AÊM
xét tam giác EAM có: EÂM=AÊM(cmt)
=>tam giác EAM cân tại M
=>ME=MA (1)
Ta có góc ACM+CÂM=90*
mà BÂM+CÂM=90*
=>góc ACM=BÂM
mà góc ACM=góc ADM( cm câu b)
=>góc ADM=DÂM
Xét tam giác MAD có góc ADM=DÂM(cmt)
=>tam giác ADM cân tại M
=>MA=MD (2)
Từ (1) và (2) suy ra MA=ME=MD
ta có định lí:trong 1 tam gáic vuông, đg trung truyến ứng với cạnh huyền bằng nửa cạnh huyền
=>MA=1/2ED
=>MA là đg trung tuyến ứng với cạnh ED
Vậy MA là đg trung tuyến của tam giác ADE

Theo định lí Pytago đảo thì:
\(3^2+4^2=5^2\)
\(9+16=25\)hợp lí
Vậy tam giác ABC vuông
Vì tam giác ABC=tam giác DEG ta có:
\(AB=DE=3cm\\ BC=EG=4cm\\ CA=GD=6cm\)