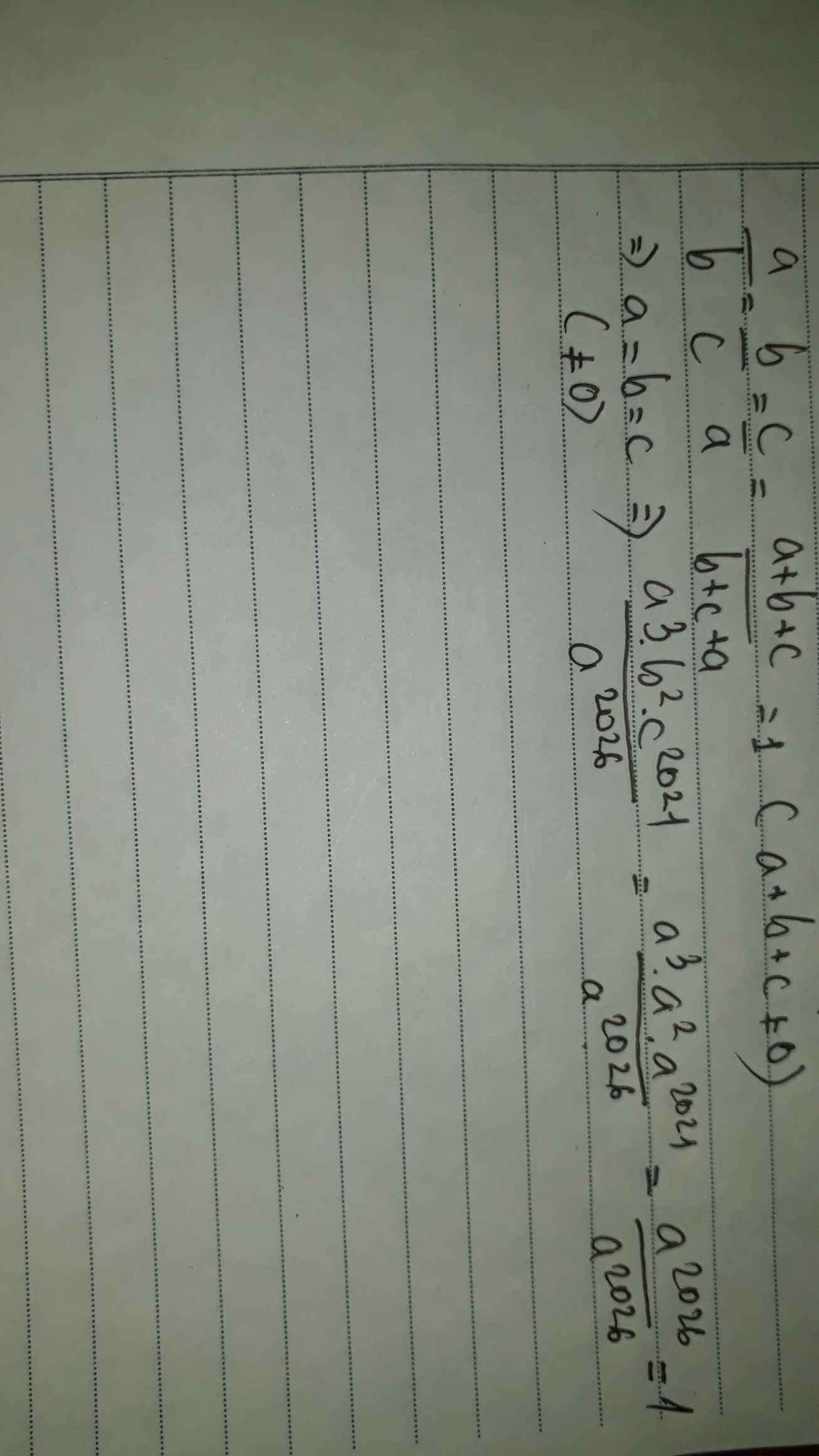Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\dfrac{3a^2-b^2}{a^2+b^2}=\dfrac{3}{4}\)
\(\Leftrightarrow4\cdot\left(3a^2-b^2\right)=3\left(a^2+b^2\right)\)
\(\Leftrightarrow12a^2-4b^2=3a^2+3b^2\)
\(\Leftrightarrow12a^2-3a^2=3b^2+4b^2\)
\(\Leftrightarrow9a^2=7b^2\)
\(\Leftrightarrow\dfrac{a^2}{b^2}=\dfrac{7}{9}\)
hay \(\dfrac{a}{b}=\pm\dfrac{\sqrt{7}}{3}\)

1. b3+b= 3
(b3+b)=3
b.(3+1)=3
b. 4= 3
b=\(\dfrac{3}{4}\)
a3+a= 3 b3
(a3+a)=3
a.(3+1)=3
a. 4= 3
a=\(\dfrac{3}{4}\)
2

\(a,\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow\dfrac{a^2}{c^2}=\dfrac{c^2}{b^2}=\dfrac{a^2+c^2}{b^2+c^2}\left(1\right)\)
Mà \(\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow ab=c^2\Leftrightarrow\dfrac{a}{b}=\dfrac{c^2}{b^2}\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\tođpcm\)
\(b,\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow ab=c^2\)
\(\Leftrightarrow\dfrac{b^2-a^2}{a^2+c^2}=\dfrac{\left(b-a\right)\left(b+a\right)}{a^2+ab}=\dfrac{\left(b-a\right)\left(b+a\right)}{a\left(a+b\right)}=\dfrac{b-a}{a}\left(đpcm\right)\)

a) vì a//b (gt) => B1 = A4 = 370 (so le trong)
b) ta có: A4 + A1 = 1800 (kề bù)
=> A1 = 1800 - A4 = 1800 - 370 = 1430
vì a//b (gt) => A1 = B2 = 1430 (đồng vị)
=> B2 = B4 = 1430 (đối đỉnh)
=> A1 = B4
c) B2 = 1430
mk ko chắc 2 câu b) và c)
768765879



Ta có: 3a2 + b2 = 4ab
<=> 3a2 + b2 - 4ab = 0
<=> a2 + b2 - 2ab + 2a2 - 2ab = 0
<=> (a - b)(3a - b) = 0 <=> a = b/3 (a - b = 0 loại vì a = b)
=> B = \(\dfrac{a-b}{a+b}\)= \(\dfrac{\dfrac{1}{3}b-b}{\dfrac{1}{3}b+b}\)= \(-\dfrac{2}{3}b:\dfrac{4}{3}b\) = \(-\dfrac{1}{2}\).

Ta có: \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}\) \(\left(a+b+c\ne0\right)\)
Áp dụng tính chất dãy tỷ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=\dfrac{a+b+c}{b+c+a}\)
Mà \(a+b+c\ne0\)
Nên: \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=1\\ \Rightarrow a=b=c\)
Thay vào biểu thức \(\dfrac{a^3.b^2.c^{2021}}{a^{2026}}\) ta được:
\(\dfrac{a^3.a^2.a^{2021}}{a^{2026}}=\dfrac{a^{2026}}{a^{2026}}=1\)
Vậy giá trị của \(\dfrac{a^3.b^2.c^{2021}}{a^{2026}}=1\)

a) Vì |a|=\(\dfrac{3}{4}\)=>a=\(\dfrac{3}{4}\).Thay vào ta sẽ có:
A=3.\(\dfrac{3}{4}\)-4.\(\dfrac{3}{4}\).(\(\dfrac{-5}{6}\))+5.(\(\dfrac{-5}{6}\))
A=\(\dfrac{9}{4}-\left(\dfrac{-5}{2}\right)+\left(\dfrac{-25}{6}\right)\)
A=\(\dfrac{19}{4}\)-\(\dfrac{25}{6}\)
A=\(\dfrac{14}{24}\)=\(\dfrac{7}{12}\)
b, Thay vào, ta sẽ có:
A=3.\(\left(\dfrac{-2}{3}\right)-4.\left(\dfrac{-2}{3}\right).\dfrac{4}{5}+5.\dfrac{4}{5}\)
A=-2-\(\left(\dfrac{-32}{15}\right)\)+4
A=\(\dfrac{2}{15}\)+4
A=\(\dfrac{62}{15}\)