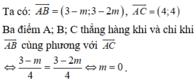DD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
22 tháng 4 2019
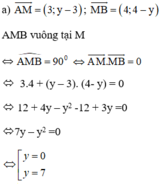
Vậy với M(5; 7) hoặc M(5; 0) thì tam giác ABM vuông tại M.
Vậy P(-5; 2)
MN
1
TD
1
18 tháng 12 2022
\(\overrightarrow{AB}=\left(1;2\right)\)
\(\overrightarrow{AC}=\left(x;y+5\right)\)
Để A,B,C thẳng hàng thì x/1=y+5/2
=>2x=y+5
=>y=2x-5
4 tháng 1
A(m-1;-1); B(2;2-2m); C(m+3;3)
\(\overrightarrow{AB}=\left(2-m+1;2-2m+1\right)\)
=>\(\overrightarrow{AB}=\left(3-m;3-2m\right)\)
\(\overrightarrow{AC}=\left(m+3-m+1;3+1\right)\)
=>\(\overrightarrow{AC}=\left(4;4\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\)
=>3-m=3-2m
=>m=0
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3-m;3-2m\right)\\\overrightarrow{AC}=\left(4;4\right)\end{matrix}\right.\)
3 điểm A;B;C thẳng hàng khi và chỉ khi \(\overrightarrow{AB}=k\overrightarrow{AC}\) với \(k\ne0\)
Hay \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\Rightarrow m=0\)
AH
Akai Haruma
Giáo viên
6 tháng 2
Lời giải:
Gọi $G(a,b)$ là trọng tâm tam giác. Ta có:
$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$
$\Leftrightarrow (1-a, 4-b)+(2-a, -3-b)+(1-a, -2-b)=(0,0)$
$\Leftrightarrow (1-a+2-a+1-a, 4-b-3-b-2-b)=(0,0)$
$\Leftrightarrow (5-3a, -1-3b)=(0,0)$
$\Rightarrow 5-3a=0; -1-3b=0$
$\Rightarrow a=\frac{5}{3}; b=\frac{-1}{3}$
b.
Để $A,B,D$ thẳng hàng thì:
$\overrightarrow{AB}=k\overrightarrow{AD}$ với $k$ là số thực $\neq 0$
$\Leftrightarrow (1,-7)=k(-2, 3m-1)$
$\Leftrightarrow \frac{1}{-2}=\frac{-7}{3m-1}$
$\Rightarrow m=5$
TD
1
18 tháng 12 2022
\(\overrightarrow{AB}=\left(-3;1\right)\)
\(\overrightarrow{AC}=\left(x-1;-5\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{x-1}{-3}=\dfrac{-5}{1}\)
=>x-1=15
=>x=16
HA
0
VD
1