Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Với \(x>0;x\ne1\)
\(P=\left(\frac{\sqrt{x}}{2}-\frac{1}{2\sqrt{x}}\right)^2\left(\frac{\sqrt{x}-1}{\sqrt{x}+1}-\frac{\sqrt{x}+1}{\sqrt{x}-1}\right)\)
\(=\left(\frac{x-1}{2\sqrt{x}}\right)^2\left(\frac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{x-1}\right)\)
\(=\frac{x^2-2x+1}{4x}.\frac{-4\sqrt{x}}{x-1}=\frac{1-x}{\sqrt{x}}\)
Thay x = 4 => \(\sqrt{x}=2\)vào P ta được :
\(\frac{1-4}{2}=-\frac{3}{2}\)
c, Ta có : \(P< 0\Rightarrow\frac{1-x}{\sqrt{x}}< 0\Rightarrow1-x< 0\)vì \(\sqrt{x}>0\)
\(\Rightarrow-x< -1\Leftrightarrow x>1\)

#)Giải :
a) Câu trc của bn mk có giải rùi, thắc mắc vô Thống kê hđ của mk xem lại nhé !
b) Để \(P>0\Rightarrow\frac{x-1}{\sqrt{x}}>0\Rightarrow x-1>0\left(\sqrt{x}>0\right)\Rightarrow x>1\)
c) Bó tay @@
\(a,P=\left(\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{1}{x-\sqrt{x}}\right):\left(\frac{1}{\sqrt{x}+1}+\frac{2}{x-1}\right)\)
\(=\left(\frac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\frac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\frac{2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\frac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\frac{\sqrt{x}-1+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{\left(x-1\right)\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\frac{x-1}{\sqrt{x}}\)
Vậy với \(x>0;x\ne1\)thì \(P=\frac{x-1}{\sqrt{x}}\)
\(b,\)Để \(P>0\Leftrightarrow\frac{x-1}{\sqrt{x}}>0\Leftrightarrow x-1>0\Leftrightarrow x>1\left(\sqrt{x}>0\right)\)

Mấy bài này dài vật vã ghê =)))))))))))))
1, a, \(\frac{3+4\sqrt{3}}{\sqrt{6}+\sqrt{2}-\sqrt{5}}\)
= \(\frac{\left(3+4\sqrt{3}\right)\left(\sqrt{6}+\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{6}+\sqrt{2}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{2}+\sqrt{5}\right)}\)
=\(\frac{\left(3+4\sqrt{3}\right)\left(\sqrt{6}+\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{6}+\sqrt{2}\right)^2-5}\)
=\(\frac{\left(3+4\sqrt{3}\right)\left(\sqrt{6}+\sqrt{2}+\sqrt{5}\right)}{8+4\sqrt{3}-5}\)
= \(\frac{\left(3+4\sqrt{3}\right)\left(\sqrt{6}+\sqrt{2}+\sqrt{5}\right)}{3+4\sqrt{3}}\)
=\(\sqrt{6}+\sqrt{2}+\sqrt{5}\)
b, M = \(\frac{\sqrt{3}\left(x-1\right)}{\sqrt{x^2}-x+1}\)(ĐKXĐ: \(x\ge0\))
= \(\frac{\sqrt{3}\left(x-1\right)}{x-x+1}\)
= \(\sqrt{3}\left(x-1\right)\)
Thay x = \(2+\sqrt{3}\)(TMĐK) vào M ta có:
M = \(\sqrt{3}\left(2+\sqrt{3}-1\right)=\sqrt{3}\left(1+\sqrt{3}\right)=3+\sqrt{3}\)
Vậy với x = \(2+\sqrt{3}\)thì M = \(3+\sqrt{3}\)
2, Mình chỉ giải câu a thôi nhé:
\(\sqrt{1+b}+\sqrt{1+c}\ge2\sqrt{1+a}\)
\(\Leftrightarrow\left(\sqrt{1+b}+\sqrt{1+c}\right)^2\ge\left(2\sqrt{1+a}\right)^2\)
\(\Leftrightarrow1+b+2\sqrt{\left(1+b\right)\left(1+c\right)}+1+c\ge4\left(1+a\right)\)
\(\Leftrightarrow2+b+c+2\sqrt{\left(1+b\right)\left(1+c\right)}\ge4\left(1+a\right)\left(1\right)\)
Vì \(\left(\sqrt{1+b}-\sqrt{1+c}\right)^2\ge0\)
\(\Rightarrow2+b+c\ge2\sqrt{\left(1+b\right)\left(1+c\right)}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow4+2\left(b+c\right)+2\sqrt{\left(1+b\right)\left(1+c\right)}\ge4\left(1+a\right)+2\sqrt{\left(1+b\right)\left(1+c\right)}\)
\(\Leftrightarrow4+2\left(b+c\right)\ge4\left(1+a\right)\)
\(\Leftrightarrow4+2\left(b+c\right)\ge4+4a\)
\(\Leftrightarrow2\left(b+c\right)\ge4a\)
\(\Leftrightarrow b+c\ge2a\)
4*. Thật ra cái này mình xài làm trội, làm giảm là được mà
Đặt A = \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+....+\frac{1}{\sqrt{n}}\)
\(\frac{1}{2}A=\frac{1}{2\sqrt{2}}+\frac{1}{2\sqrt{3}}+....+\frac{1}{2\sqrt{n}}\)
\(\frac{1}{2}A=\frac{1}{\sqrt{2}+\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{3}}+....+\frac{1}{\sqrt{n}+\sqrt{n}}\)
Ta có: \(\frac{1}{\sqrt{2}+\sqrt{2}}>\frac{1}{\sqrt{3}+\sqrt{2}}\)
\(\frac{1}{\sqrt{3}+\sqrt{3}}>\frac{1}{\sqrt{4}+\sqrt{3}}\)
+ .........................................................
\(\frac{1}{\sqrt{n}+\sqrt{n}}>\frac{1}{\sqrt{n+1}+\sqrt{n}}\)
Cộng tất cả vào
\(\Rightarrow\frac{1}{\sqrt{2}+\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{3}}+...+\frac{1}{\sqrt{n}+\sqrt{n}}>\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}+...+\frac{1}{\sqrt{n+1}+\sqrt{n}}\)\(\frac{1}{2}A>\frac{\sqrt{3}-\sqrt{2}}{3-2}+\frac{\sqrt{4}-\sqrt{3}}{4-3}+...+\frac{\sqrt{n+1}-\sqrt{n}}{n+1-n}\)
\(\frac{1}{2}A>\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+...+\sqrt{n+1}-\sqrt{n}\)
\(\frac{1}{2}A>\sqrt{n+1}-\sqrt{2}\)
\(A>2\sqrt{n+1}-2\sqrt{2}>2\sqrt{n+1}-3\)
\(A+1>2\sqrt{n+1}-3+1\)
\(A+1>2\sqrt{n+1}-2\)
\(A+1>2\left(\sqrt{n+1}-1\right)\)
Vậy ta có điều phải chứng minh.
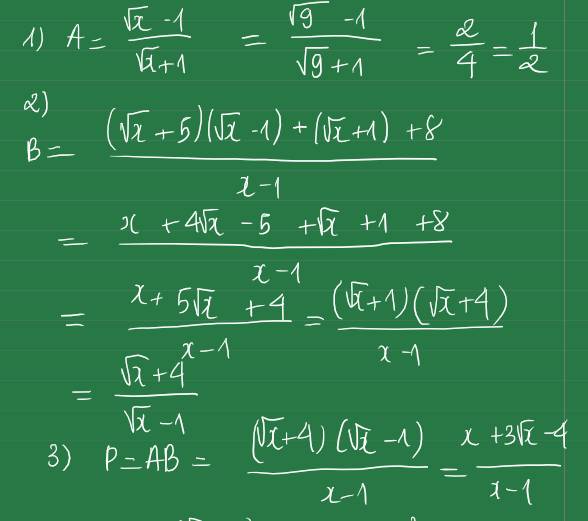
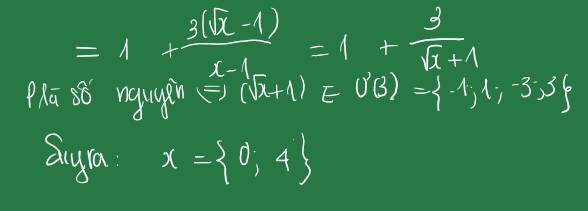
\(a,P=A:B=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{x-1}{\sqrt{x}+1}=\dfrac{\left(x-1\right)^2}{\sqrt{x}\left(x-1\right)}=\dfrac{x-1}{\sqrt{x}}\\ b,P\sqrt{x}=m+\sqrt{x}\\ \Leftrightarrow x-1=m+\sqrt{x}\\ \Leftrightarrow x-\sqrt{x}-m-1=0\)
Để tồn tại x thì PT phải có nghiệm hay \(\Delta=1-4\left(-m-1\right)\ge0\)
\(\Leftrightarrow4m+5\ge0\\ \Leftrightarrow m\ge-\dfrac{5}{4}\)