Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tính BC:
Áp dụng định lí Py-tago vào \(\Delta\)vuông ABC
ta có: BC2=BA2+AC2
=>BC2= 62+82
=> BC2= 36+64
=>BC2= 100
=> BC= \(\sqrt{100}\)
=> BC= 10 (cm)
b)c/m \(\Delta\)HAB đồng dạng \(\Delta\)HCA:
Ta có: - tam giác HAB đồng dạng với tam giác ABC ( \(\widehat{B}\)chung)
- tam giác HAC đồng dạng với tam giác ABC ( \(\widehat{C}\)chung)
=> \(\Delta HAB\)đồng dạng \(\Delta HCA\)( cùng đồng dạng \(\Delta ABC\))
có bạn nào giúp minh câu c và d được k. mình k cho

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)(hệ thức lượng)
b: BC=BH+CH=13(cm)
\(AB=\sqrt{BH\cdot BC}=2\sqrt{13}\left(cm\right)\)
\(AC=\sqrt{9\cdot13}=3\sqrt{13}\left(cm\right)\)

a)Xét tam giác HAC và tam giác ABC có :
Góc AHC = góc BAC ( = 90o)
Góc BCA chung
⇒ Tam giác HAC ~ Tam giác ABC ( TH3 )
b) Xét tam giác AHD và tam giác ABH có :
Góc HAB chung
Góc ADH = Góc AHB ( = 90o)
⇒ Tam giác AHD ~ Tam giác ABH ( TH3)
⇒ \(\dfrac{AH}{AB}=\dfrac{AD}{AH}\)
⇒ AH2 = AB.AD
c) Xét tam giác AEH và tam giác AHC có :
Góc HAC chung
Góc AEH = góc AHC ( = 90o)
⇒ Tam giác AEH ~ Tam giác AHC ( TH3)
⇒ \(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)
⇒ AH2 = AE.AC
Mà : AH2 = AD.AB ( Câu b)
⇒ AE.AC = AD.AB
d) Do : AE.AC = AD.AB ( Câu c)
⇒ \(\dfrac{AE}{AD}=\dfrac{AC}{AB}\)
Xét tam giác AED và tam giác ACB có :
Góc BAC chung
\(\dfrac{AE}{AD}=\dfrac{AC}{AB}\) ( cmt)
⇒Tam giác AED ~ Tam giác ACB ( TH2)
⇒ \(\dfrac{S_{AED}}{S_{ACB}}=\left(\dfrac{AE}{AC}\right)^2\)
P/S : Hình như thiếu dữ kiện , chưa cho AH nên ko ra số cụ thể
â)xét tam giác hac và tam giác abc có:
góc c chung
góc ahc= góc bac=90 độ
suy ra tam giác hac đồng dạng với tam giác abc(g.g)
b)xét tam giác ahb và tam giác adh có
góc ahb= góc adh=90 độ
góc a chung
suy ra tam giác ahb đồng dạng với tam giác adh(g.g)
ta có:ah^2=ab.ad

Lời giải:
a)
Vì $M, N$ lần lượt là trung điểm của $AB,AC$ nên:
\(\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{2}\)
Xét tam giác $AMN$ và $ABC$ có:
\(\left\{\begin{matrix} \text{chung góc A}\\ \frac{AM}{AB}=\frac{AN}{AC}\end{matrix}\right.\Rightarrow \triangle AMN\sim \triangle ABC\) (c.g.c)
b)
Áp dụng định lý Pitago cho tam giác vuông $ABC$:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{9^2+12^2}=15\) (cm)
Ta có:
\(\frac{AB.AC}{2}=S_{ABC}=\frac{AH.BC}{2}\)
\(\Rightarrow AH=\frac{AB.AC}{BC}=\frac{9.12}{15}=7,2\) (cm)
c)
Vì \(NP\parallel AB\) nên áp dụng định lý Ta-lét ta có:
\(\frac{NP}{AB}=\frac{CN}{CA}=\frac{1}{2}\Rightarrow NP=\frac{AB}{2}; NC=\frac{AC}{2}\)
Mặt khác, \(NP\parallel AB, AB\perp AC\Rightarrow NP\perp AC\)
Do đó:
\(S_{NPC}=\frac{NP.NC}{2}=\frac{\frac{AB}{2}.\frac{AC}{2}}{2}=\frac{AB.AC}{8}\)
\(S_{ABC}=\frac{AB.AC}{2}\)
\(\Rightarrow \frac{S_{NPC}}{S_{ABC}}=\frac{AB.AC}{8}: \frac{AB.AC}{2}=\frac{1}{4}\)
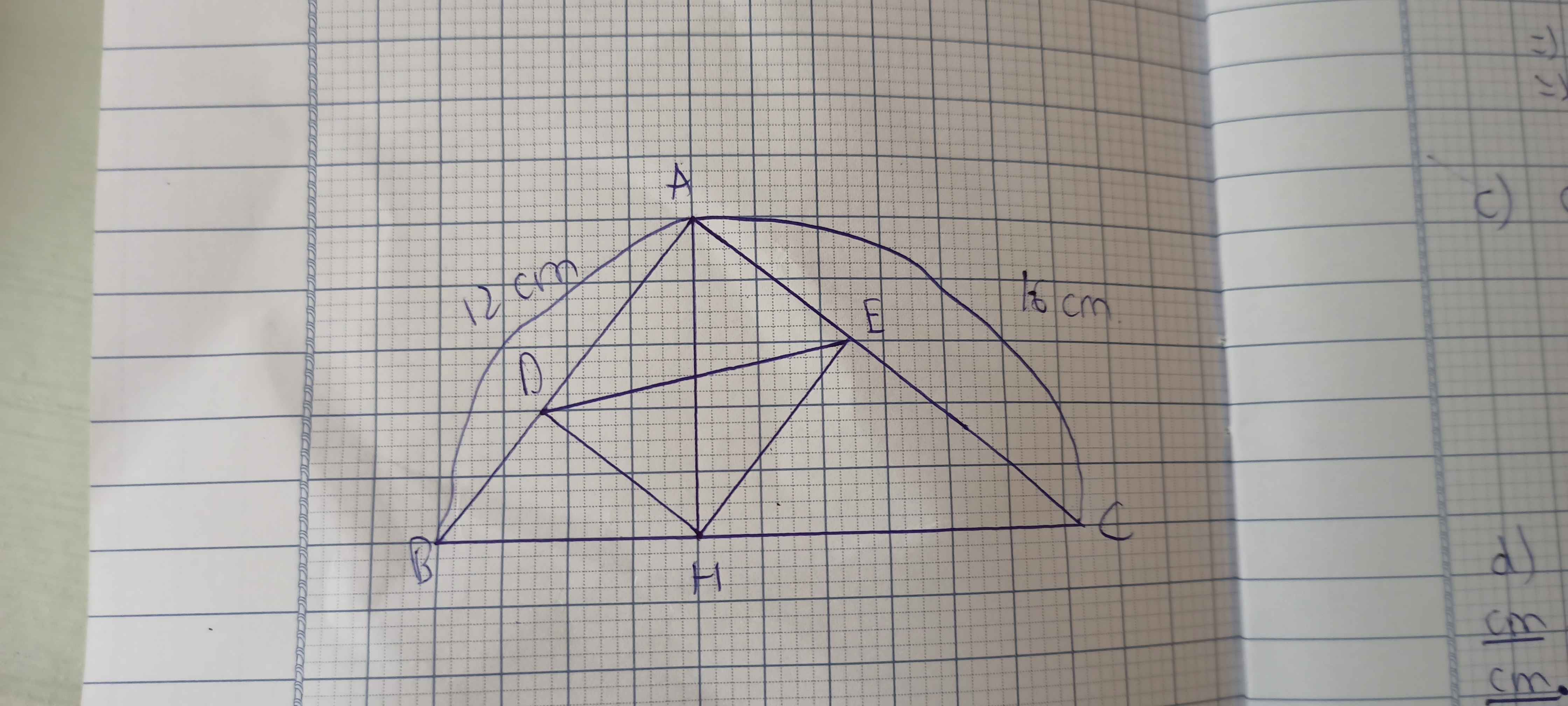


-△ABH∼△CBA (g-g) \(\Rightarrow\dfrac{AB}{CB}=\dfrac{BH}{BA}\Rightarrow BH=\dfrac{AB^2}{CB}\)
-△CAH∼△CBA (g-g) \(\Rightarrow\dfrac{CA}{CB}=\dfrac{CH}{CA}\Rightarrow CH=\dfrac{AC^2}{CB}\)
\(\dfrac{S_{HAB}}{S_{HAC}}=\dfrac{HB}{HC}=\dfrac{\dfrac{AB^2}{CB}}{\dfrac{AC^2}{CB}}=\left(\dfrac{AB}{AC}\right)^2=\left(\dfrac{4}{9}\right)^2=\dfrac{36}{81}\)