
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$a^2+b^2+c^2-ab-bc-ac=0$
$\Leftrightarrow 2a^2+2b^2+2c^2-2ab-2bc-2ac=0$
$\Leftrightarrow (a^2-2ab+b^2)+(b^2-2bc+c^2)+(c^2-2ac+a^2)=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
Vì $(a-b)^2; (b-c)^2; (c-a)^2\geq 0$ với mọi $a,b,c$ nên để tổng của chúng bằng $0$ thì:
$a-b=b-c=c-a=0$
$\Rightarrow a=b=c$
$\Rightarrow \frac{a}{b}=\frac{b}{c}=\frac{c}{a}=1$
Khi đó:
$(\frac{a}{b}+1)(\frac{b}{c}+1)(\frac{c}{a}+1)=(1+1)(1+1)(1+1)=8$
Ta có đpcm.


Ta có: a+b+c=0
nên a+b=-c
Ta có: \(a^2-b^2-c^2\)
\(=a^2-\left(b^2+c^2\right)\)
\(=a^2-\left[\left(b+c\right)^2-2bc\right]\)
\(=a^2-\left(b+c\right)^2+2bc\)
\(=\left(a-b-c\right)\left(a+b+c\right)+2bc\)
\(=2bc\)
Ta có: \(b^2-c^2-a^2\)
\(=b^2-\left(c^2+a^2\right)\)
\(=b^2-\left[\left(c+a\right)^2-2ca\right]\)
\(=b^2-\left(c+a\right)^2+2ca\)
\(=\left(b-c-a\right)\left(b+c+a\right)+2ca\)
\(=2ac\)
Ta có: \(c^2-a^2-b^2\)
\(=c^2-\left(a^2+b^2\right)\)
\(=c^2-\left[\left(a+b\right)^2-2ab\right]\)
\(=c^2-\left(a+b\right)^2+2ab\)
\(=\left(c-a-b\right)\left(c+a+b\right)+2ab\)
\(=2ab\)
Ta có: \(M=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)
\(=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
\(=\dfrac{a^3+b^3+c^3}{2abc}\)
Ta có: \(a^3+b^3+c^3\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ca-cb+c^2\right)-3ab\left(a+b\right)\)
\(=-3ab\left(a+b\right)\)
Thay \(a^3+b^3+c^3=-3ab\left(a+b\right)\) vào biểu thức \(=\dfrac{a^3+b^3+c^3}{2abc}\), ta được:
\(M=\dfrac{-3ab\left(a+b\right)}{2abc}=\dfrac{-3\left(a+b\right)}{2c}\)
\(=\dfrac{-3\cdot\left(-c\right)}{2c}=\dfrac{3c}{2c}=\dfrac{3}{2}\)
Vậy: \(M=\dfrac{3}{2}\)

\(ab+bc+ca=0\)
=> \(\frac{ab+bc+ca}{abc}=0\)
=> \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)
Đặt: \(\frac{1}{a}=x;\)\(\frac{1}{b}=y;\)\(\frac{1}{c}=z\)
Ta có: \(x+y+z=0\)
=> \(x^3+y^3+z^3=3xyz\) (tự c/m, ko c/m đc ib)
hay \(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)
\(B=\frac{bc}{a^2}+\frac{ca}{b^2}+\frac{ab}{c^2}=\frac{abc}{a^3}+\frac{abc}{b^3}+\frac{abc}{c^3}=abc.\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)\)
\(=abc.\frac{3}{abc}=3\)

a) Áp dụng Cauchy Schwars ta có:
\(M=\frac{a^2}{a+1}+\frac{b^2}{b+1}+\frac{c^2}{c+1}\ge\frac{\left(a+b+c\right)^2}{a+b+c+3}=\frac{9}{6}=\frac{3}{2}\)
Dấu "=" xảy ra khi: a = b = c = 1
b) \(N=\frac{1}{a}+\frac{4}{b+1}+\frac{9}{c+2}\ge\frac{\left(1+2+3\right)^2}{a+b+c+3}=\frac{36}{6}=6\)
Dấu "=" xảy ra khi: x=y=1

Do a+b+c= 0
<=> a+b= -c
=> (a+b)2= c2
Tương tự: (c+a)2= b2, (c+b)2= a2
Ta có: \(A=\frac{1}{b^2+c^2-a^2}+\frac{1}{c^2+a^2-b^2}+\frac{1}{a^2+b^2-c^2}\)
\(=\frac{1}{b^2+c^2-\left(b+c\right)^2}+\frac{1}{c^2+a^2-\left(c+a\right)^2}+\frac{1}{a^2+b^2-\left(a+b\right)^2}\)
\(=\frac{1}{-2bc}+\frac{1}{-2ca}+\frac{1}{-2ab}\)
\(=\frac{a+b+c}{-2abc}=0\)

Ta có :
\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab-2bc-2ac\)
mà theo đề bài \(a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-ab-bc-ac=0\)
\(\Rightarrow\left(a-b-c\right)^2=-\left(ab+bc+ac\right)=0\)
mà \(-\left(ab+bc+ac\right)\le0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow dpcm\)

(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
⇒ 2ab + 2bc + 2ac = (a + b + c)2 - (a2 + b2 + c2)
⇒ 2.(ab + bc + ac) = 92 - 53
2.(ab + bc + ac) = 81 - 53
2.(ab + bc + ac) = 28
ab + bc + ac = 28 : 2
ab + bc + ac = 14
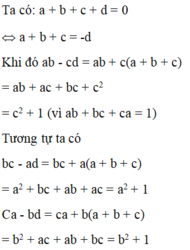

Câu hỏi của Conan Kudo - Toán lớp 8 - Học toán với OnlineMath
Bạn tham khảo nhé!