Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: \(\widehat{C}=90^0-60^0=30^0\)
Xét ΔABC có \(\widehat{C}< \widehat{B}\)
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
Do đó: ΔAHC=ΔDHC
c: Xét ΔBAC và ΔBDC có
CA=CD
\(\widehat{ACB}=\widehat{DCB}\)
CB chung
Do đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)
a: \(\widehat{C}=90^0-60^0=30^0\)
Xét ΔABC có \(\widehat{C}< \widehat{B}\)
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
Do đó: ΔAHC=ΔDHC
c: Xét ΔBAC và ΔBDC có
CA=CD
\(\widehat{ACB}=\widehat{DCB}\)
CB chung
Do đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)
a: Xét ΔCAD có
CH vừa là đường cao, vừa là trung tuyến
=>ΔCAD cân tại C
b: Xet ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
=>ΔCAB=ΔCDB
a: Xét ΔCAD có
CH vừa là đường cao, vừa là trung tuyến
=>ΔCAD cân tại C
b: Xet ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
=>ΔCAB=ΔCDB
a) Xét ΔABH vuông tại H và ΔDBH vuông tại H có
BH chung
HA=HD(gt)
Do đó: ΔABH=ΔDBH(hai cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
mà tia BH nằm giữa hai tia BA,BD
nên BH là tia phân giác của \(\widehat{ABD}\)(đpcm)
b) Xét ΔACH vuông tại H và ΔDCH vuông tại H có
CH chung
AH=DH(gt)
Do đó: ΔACH=ΔDCH(hai cạnh góc vuông)
Suy ra: CA=CD(hai cạnh tương ứng)
Ta có: ΔABH=ΔDBH(cmt)
nên BA=BD(hai cạnh tương ứng)
Xét ΔABC và ΔDBC có
BA=BD(cmt)
BC chung
CA=CD(cmt)
Do đó: ΔABC=ΔDBC(c-c-c)
Bạn tự vẽ hình nha =="
a.
Tam giác ABC vuông tại A có:
ABC + ACB = 900
600 + ACB = 900
ACB = 900 - 600
ACB = 300
ABC > ACB (600 > 300)
=> AC > AB (quan hệ giữa góc và cạnh đối diện trong tam giác)
=> HC > BH (quan hệ giữa đường xiên và hình chiếu trong tam giác)
b.
Xét tam giác AHC và tam giác DHC có:
AH = DH (gt)
AHC = DHC ( = 900)
HC là cạnh chung
=> Tam giác AHC = Tam giác DHC (c.g.c)
c.
Xét tam giác ABC và tam giác DBC có:
AC = DC (Tam giác AHC = Tam giác DHC)
ACB = DCB (Tam giác AHC = Tam giác DHC)
CB là cạnh chung
=> Tam giác ABC = Tam giác DBC (c.g.c)
=> BAC = BDC (2 góc tương ứng)
mà BAC = 900
=> BDC = 900
Chúc bạn học tốt ^^
a) Xét t/giác BAH và t./giác CAH có
AHB=AHC (=90 độ)
AH là cạnh chung
AB=AC( t/giác ABC cân tại A)
Do đó t/giác BAH= t/giácCAH(chcgv)
suy ra HB=HC(2 cạnh t/ứ)
BAH=CAH(2 góc tương ứng)
suy ra AH là tia pg của BAC
b)Xét t/giác DBE và t/giác HBA có
AB=AE(gt)
DB=DH(gt)
ABH=DBE( 2 góc đối đỉnh)
Do đó t/giác DBE= t/giác HBA(cgc)
suy ra BAH=BED( 2 góc t/ứ)
Mà BAH và BED là 2 góc ở vị trí SLT của 2 đường thẳng AH và DE
suy ra AH//DE
c) Ta có DH=DB+BH
suy ra DH=2BH ( DB=BH)
Do đó DH>BH
Mà DH đối diện với góc DAH
BH đối diện với hóc BAH
suy ra DAH>BAH
( sr mình ko bt lm câu d 
)
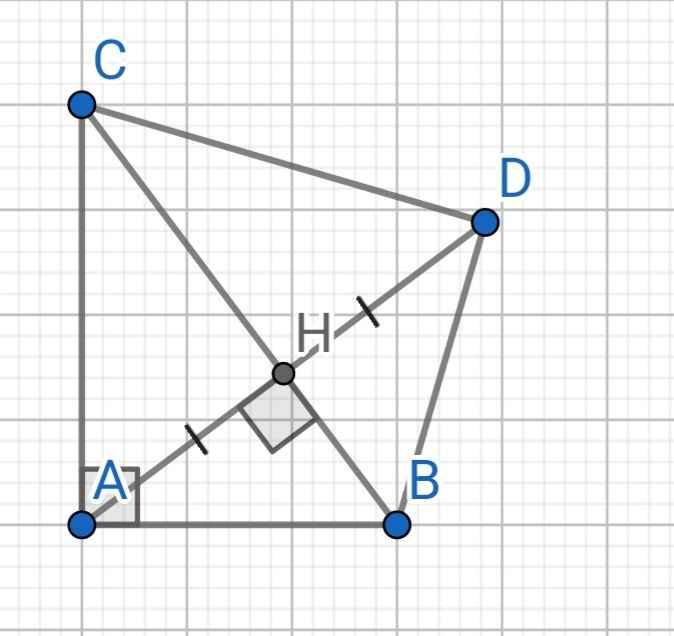a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:
BH là cạnh chung
HA = HD (gt)
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
⇒ BH là tia phân giác của ∠ABD
b) Do ∆ABH = ∆DBH (cmt)
⇒ AB = DB (hai cạnh tương ứng)
Do ∠ABH = ∠DBH (cmt)
⇒ ∠ABC = ∠DBC
Xét ∆ABC và ∆DBC có:
AB = DB (cmt)
∠ABC = ∠DBC (cmt)
AC là cạnh chung
⇒ ∆ABC = ∆DBC (c-g-c)
c) Do ∆ABC = ∆DBC (cmt)
⇒ ∠BAC = ∠BDC = 90⁰ (hai góc tương ứng)
⇒ BD ⊥ CD
a: Xét ΔBAC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔDBC có BH<CH
mà BH là hình chiếu của DB trên BC
và CH là hình chiếu của DC trên BC
nên DB<DC
=>\(\widehat{DCB}< \widehat{DBC}\)