Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHMK có góc AHM=góc AKM=góc KAH=90 độ
nên AHMK là hìh chữ nhật
=>MD vuông góc với ME
b: Xét tứ giác AKHD có
AK//HD
AK=HD
DO đó: AKHD là hình bình hành
=>KH//AD và KH=AD
Xét ΔMED có MK/ME=MH/MD
nên KH//ED và KH=ED/2
=>AD//ED và AD=ED/2
=>E,A,D thẳng hàng
mà ED=2AD
nên A là trung điểm của ED
c: Xét ΔBAC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
=>HA=HB=MK
d: Xét tứ giác AMBD có
H là trung điểm chung của AB vàMD
MA=MB
Do đó: AMBD là hình thoi
=>AM//BD và AM=BD
Xét tứ giác AMCE có
K là trung điểm chubg của AC và ME
nên AMCE là hình bình hành
=>AM//CE và AM=CE
=>BD//CE và BD=CE

a: Xét tứ giác AHMK có góc AHM=góc AKM=góc KAH=90 độ
nên AHMK là hìh chữ nhật
=>MD vuông góc với ME
b: Xét tứ giác AKHD có
AK//HD
AK=HD
DO đó: AKHD là hình bình hành
=>KH//AD và KH=AD
Xét ΔMED có MK/ME=MH/MD
nên KH//ED và KH=ED/2
=>AD//ED và AD=ED/2
=>E,A,D thẳng hàng
mà ED=2AD
nên A là trung điểm của ED
c: Xét ΔBAC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
=>HA=HB=MK

a: Xét tứ giác AHMK có góc AHM=góc AKM=góc KAH=90 độ
nên AHMK là hìh chữ nhật
=>MD vuông góc với ME
b: Xét tứ giác AKHD có
AK//HD
AK=HD
DO đó: AKHD là hình bình hành
=>KH//AD và KH=AD
Xét ΔMED có MK/ME=MH/MD
nên KH//ED và KH=ED/2
=>AD//ED và AD=ED/2
=>E,A,D thẳng hàng
mà ED=2AD
nên A là trung điểm của ED
c: Xét ΔBAC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
=>HA=HB=MK

a: Xét tứ giá AHMK có góc AHM=góc AKM=góc KAH=90 độ
nên AHMK là hình chữ nhật
=>MK vuông góc với MH
=>ME vuông góc với MD
b: Xét ΔAMD có
AB vừa là đường cao, vừa là trung tuyến
nên ΔAMD cân tại A
=>AB là phân giác của góc MAD(1)
Xét ΔAME có
AC vừa là đường cao, vừa là trung tuyến
nên ΔAME cân tại A
=>AC là phân giác của góc MAE(2)
Từ (1) và (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
c: Xét ΔBAC có
M là trung điểm của BC
MH//AC
DO đó:H là trung điểm của AB
=>AH=HB=MK
d: Xét tứ giác AMBD có
H là trung điểm chung của AB và MD
nên AMBD là hình bình hành
=>AM//BD và AM=BD
Xét tứ giác AMCE có
K là trung điểm của AC và ME
nên AMCE là hình bình hành
=>CE//AM và CE=AM
=>BD//CE và BD=EC

a: Xét tứ giá AHMK có góc AHM=góc AKM=góc KAH=90 độ
nên AHMK là hình chữ nhật
=>MK vuông góc với MH
=>ME vuông góc với MD
b: Xét ΔAMD có
AB vừa là đường cao, vừa là trung tuyến
nên ΔAMD cân tại A
=>AB là phân giác của góc MAD(1)
Xét ΔAME có
AC vừa là đường cao, vừa là trung tuyến
nên ΔAME cân tại A
=>AC là phân giác của góc MAE(2)
Từ (1) và (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
c: Xét ΔBAC có
M là trung điểm của BC
MH//AC
DO đó:H là trung điểm của AB
=>AH=HB=MK
d: Xét tứ giác AMBD có
H là trung điểm chung của AB và MD
nên AMBD là hình bình hành
=>AM//BD và AM=BD
Xét tứ giác AMCE có
K là trung điểm của AC và ME
nên AMCE là hình bình hành
=>CE//AM và CE=AM
=>BD//CE và BD=EC

a: Xét tứ giác AKMH có
\(\widehat{AKM}=\widehat{AHM}=\widehat{HAK}=90^0\)
Do đó: AKMH là hình chữ nhật
Suy ra: MD⊥ME
Anh lm cái trò j vậy? Đây là \(\Delta\) chứ ko phải tứ giác

a/
Xét tg MAB và tg MEC có
MB=MC (gt); MA=ME (gt)
\(\widehat{AMB}=\widehat{EMC}\) (góc đối đỉnh)
=> tg MAB = tg MEC (c.g.c)
b/
Ta có tg MAB = tg MEC (cmt) \(\Rightarrow\widehat{BAM}=\widehat{CEM}\)
Hai góc trên ở vị trí so le trong => AB//CE
c/
Xét tg vuông ABH và tg vuông DBH có
HA=HD (gt); BH chung => tg ABH = tg DBH (hai tg vuông có 2 cạnh góc vuông bằng nhau) => AB=BD(1)
Ta có tg MAB = tg MEC (cmt) => AB=CE (2)
Từ (1) và (2) => BD=CE
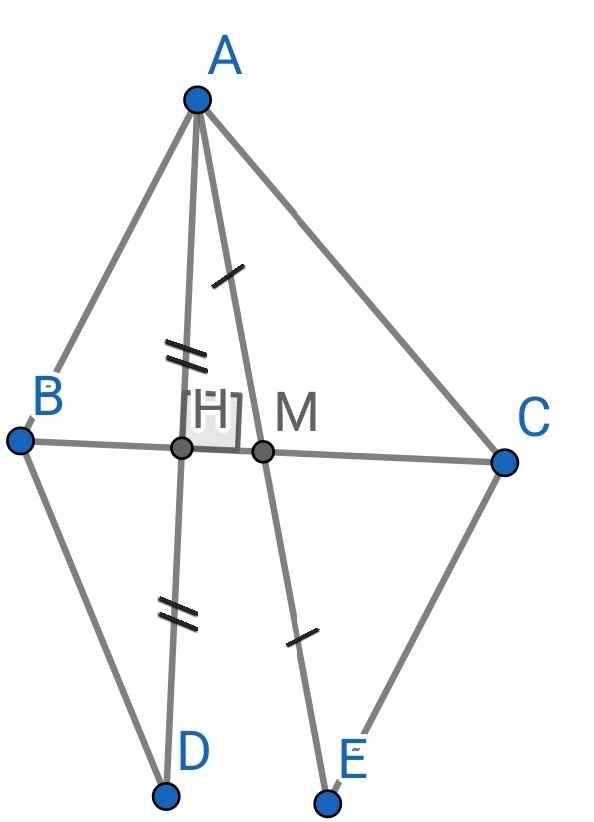 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Xét ∆MAB và ∆MEC có:
BM = MC (cmt)
∠AMB = ∠EMC (đối đỉnh)
AM = ME (gt)
⇒ ∆MAB = ∆MEC (c-g-c)
b) Do ∆MAB = ∆MEC (cmt)
⇒ ∠MAB = ∠MEC (hai góc tương ứng)
Mà ∠MAB và ∠MEC là hai góc so le trong)
AB // CE
c) Xét hai tam giác vuông: ∆AHB và ∆DHB có:
BH là cạnh chung
AH = HD (gt)
⇒ ∆AHB = ∆DHB (hai cạnh góc vuông)
⇒ AB = BD (hai cạnh tương ứng)
Do ∆MAB = ∆MEC (cmt)
⇒ AB = CE (hai cạnh tương ứng)
Mà AB = BD (cmt)
⇒ BD = CE
a: Xét tứ giá AHMK có góc AHM=góc AKM=góc KAH=90 độ
nên AHMK là hình chữ nhật
=>MK vuông góc với MH
=>ME vuông góc với MD
b: Xét ΔAMD có
AB vừa là đường cao, vừa là trung tuyến
nên ΔAMD cân tại A
=>AB là phân giác của góc MAD(1)
Xét ΔAME có
AC vừa là đường cao, vừa là trung tuyến
nên ΔAME cân tại A
=>AC là phân giác của góc MAE(2)
Từ (1) và (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
c: Xét ΔBAC có
M là trung điểm của BC
MH//AC
DO đó:H là trung điểm của AB
=>AH=HB=MK
d: Xét tứ giác AMBD có
H là trung điểm chung của AB và MD
nên AMBD là hình bình hành
=>AM//BD và AM=BD
Xét tứ giác AMCE có
K là trung điểm của AC và ME
nên AMCE là hình bình hành
=>CE//AM và CE=AM
=>BD//CE và BD=EC