Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

| GT | △ABC . BE ⊥ AC, CF ⊥ AB. BE = CF = 8 cm BF và BC tỉ lệ 3 và 5 BE ∩ CF = {O} . Nối AO với EF |
KL | a, △ABC cân b, BC = ? c, AO là trung trực EF |
Bài làm:
a, Xét △BFC vuông tại F và △CEB vuông tại E
Có: BC là cạnh chung
CF = BE (gt)
=> △BFC = △CEB (ch-cgv)
=> FBC = ECB (2 góc tương ứng)
Xét △ABC có: ABC = ACB (cmt)
=> △ABC cân tại A
b, Gọi độ dài của cạnh BF và BC là a, b (cm, a, b > 0)
Theo bài ra, ta có: \(\frac{a}{3}=\frac{b}{5}\)\(\Rightarrow b=\frac{5a}{3}\)
Xét △FBC vuông tại F có: \(BC^2=BF^2+FC^2\)(định lý Pitago)
\(\Rightarrow b^2=a^2+8^2\)\(\Rightarrow\left(\frac{5a}{3}\right)^2=a^2+64\)\(\Rightarrow\frac{25}{9}.a^2-a^2=64\)
\(\Rightarrow a^2\left(\frac{25}{9}-1\right)=64\)\(\Rightarrow a^2.\frac{16}{9}=64\)\(\Rightarrow a^2=64\div\frac{16}{9}=36\)\(\Rightarrow a=6\)
\(\Rightarrow b=\frac{5}{3}a=\frac{5}{3}.6=10\)\(\Rightarrow BC=10\)(cm)
c, Vì △ABC cân tại A => AB = AC
Ta có: AB = AF + FB
BC = AE + EC
Mà AB = AC (cmt) ; BF = EC (△BFC = △CEB)
=> AF = AE
=> A thuộc đường trung trực của FE (1)
Ta có: DBC = FBE + EBC
ECB = ECF + FCB
Mà DBC = ECB (cmt); BCF = EBC (△BFC = △CEB)
=> FBE = ECF
Xét △BFO vuông tại F và △CEO vuông tại E
Có: FBO = ECO (cmt)
BF = CE (△BFC = △CEB)
=> △BFO = △CEO (cgv-gnk)
=> FO = OE (2 cạnh tương ứng)
=> O thuộc đường trung trực của FE (2)
Từ (1) và (2) => đường thẳng AO là trung trực của EF.

a/ Xét tam giác ABC có 2 đường trung tuyến BE;CF cắt nhau tại I => I là trọng tâm tam giác ABC
=> AI là đường trung tuyến thứ 3
=> AI đi qua trung điểm H của BC
=> HB = HC
Mà tam giác ABC cân tại A => AI vừa là đường trung tuyến vừa là đường phân giác => góc BAH = góc CAH
Xét tam giác ABI và tam giác CAI có:
\(\hept{\begin{cases}\widehat{BAI}=\widehat{CAI}\left(cmt\right)\\AB=AC\left(gt\right)\\AI:chung\end{cases}}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABI}=\widehat{ACI}\)
Mà: \(\widehat{ABC}=\widehat{ACB}\left(gt\right)\)
\(\Rightarrow\widehat{IBC}=\widehat{ICB}\)
=> Tam giác BIC cân tại I
b/ Vì I là trọng tâm tam giác ABC => \(BI=\frac{2}{3}BE;IE=\frac{1}{3}BE\Rightarrow BI=\frac{2}{3}:\frac{1}{3}=2IE\)
Vì tam giác ABC cân tại A => AI vừa là đường trung tuyến vừa là đường cao
=> AI vuông góc BC tại H
Xét tam giác BIH vuông tại H có BI là cạnh huyền => \(BH< BI\Rightarrow BH< 2IE\left(1\right)\)
Giải thích thêm: Vì AB = AC (gt) mà F là trung điểm AB; E là trung điểm AC => \(AF=BF=AE=CE\)
Xét tam giác BFC và tam giác BEC có:
\(\hept{\begin{cases}BC:chung\\\widehat{ABC}=\widehat{ACB}\left(gt\right)\\BF=EC\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta BFC=\Delta CEB\left(c.g.c\right)\)
\(\Rightarrow CF=BE\)
Vì I là trọng tâm tam giác ABC => \(CI=\frac{2}{3}CF;IF=\frac{1}{3}CF\Rightarrow CI=\frac{2}{3}:\frac{1}{3}=2CF\)
Xét tam giác HIC vuông tại H có CI là cạnh huyền => \(CH< CI\Rightarrow CH< 2IF\)
Mà: \(BE=CF\left(cmt\right)\Rightarrow HC< 2IE\left(2\right)\)
Từ (1);(2) \(\Rightarrow HB+HC< 2IE+2IE\)
\(\Rightarrow BC< 4IE\left(cmt\right)\)
PS: Check lại nha bạn
Có mỗi chỗ 2IF mà cậu nhầm thành 2CF thôi,còn lại đúng hết.Cảm ơn vì đã giải
Định k cho cậu mà oniline math nó không cho TT^TT

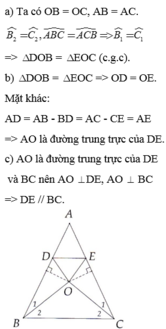
a,Xét tam giác vuông ABD vuông tại D và tam giác ACE vuông tại E có AB=AC (GT), góc BAD chung , Góc E = Góc D =90 độ (gt)
=> Tam giác vuông ABD =Tam giác ACE (c.h-g.n) =>BD=CE ( 2 cạnh tg ứng )
b, Có góc B=góc C (tam giác ABC cân) mà góc B = góc B1+góc B2 góc C =góc C1+ góc Lại có B1=C1 ( tam giác ABD= tam giác ACE ) Góc B= góc C => góc B2= góc C2 => Tam giác BHC cân tại B
a: Xét ΔFBC vuông tại F và ΔECB vuông tại E có
BC chung
\(\widehat{FBC}=\widehat{ECB}\)(ΔABC cân tại A)
Do đó: ΔFBC=ΔECB
b: Ta có;ΔFBC=ΔECB
=>\(\widehat{OBC}=\widehat{OCB}\)
=>ΔOBC cân tại O
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(1)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AO là đường trung trực của BC