K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 3 2023
`a)`
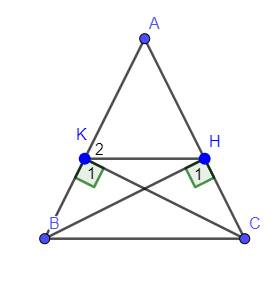
+, Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=hat(ACB)`
hay `hat(KBC)=hat(HCB)`
Xét `Delta BHC` và `Delta CKB` có :
`{:(hat(H_1)=hat(K_1)(=90^0)),(BC-chung),(hat(HCB)=hat(KBC)(cmt)):}}`
`=>Delta BHC=Delta CKB(c.h-g.n)(đpcm)`
+, Có `Delta BHC=Delta CKB(cmt)`
`=>HC=BK` ( 2 cạnh t/ứng )
mà `AB=AC(Delta ABC` cân tại `A)`
nên `AB-BK=AC-CH`
hay `AK=AH`
`=>Delta AHK` cân tại `A(đpcm)`
`b)`
Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=(180^0-hat(A))/2` (1)
`Delta AHK ` cân tại `A(cmt)=>hat(K_2)=(180^0-hat(A))/2` (2)
Từ (1) và (2) suy ra :
`hat(ABC)=hat(K_2)`
mà `2` góc này ở vị trí Đồng vị
nên `KH////BC(đpcm)`
12 tháng 5 2022
a: Xét ΔADB và ΔADC có
AD chung
\(\widehat{BAD}=\widehat{CAD}\)
AB=AC
Do đó: ΔADB=ΔADC
12 tháng 5 2022
Xét `2 Delta ADB, ADC`:
`AD` chung
`AB = AC`.
`hat(DAB) = hat(DAC)`
`=> Delta ADB = Delta ADC`.
28 tháng 4 2021
a) Xét \(\Delta ABI\) và\(\Delta ACI\) có
góc B= góc C(gt)
AB=AC(gt)
góc BAI =góc CAI(AI là p/g góc A)
Vậy \(\Delta ABI\) =\(\Delta ACI\) (g.c.g)
28 tháng 4 2021
a) Xét ΔABI và ΔACI có
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
AB=AC(ΔABC cân tại A)
\(\widehat{BAI}=\widehat{CAI}\)(AI là tia phân giác của \(\widehat{BAC}\)
Do đó: ΔABI=ΔACI(g-c-g)
và gì nữa bn