K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
0
VT
4 tháng 1 2018
Từ giả thiết, ta có \(cd\left(a^2+b^2\right)=ab\left(c^2+d^2\right)\Leftrightarrow a^2cd+b^2cd-abc^2-abd^2=0\)
<=>\(\left(a^2cd-abc^2\right)+\left(b^2cd-abd^2\right)=0\Leftrightarrow ac\left(ad-bc\right)+bd\left(bc-ad\right)=0\)
<=>\(ac\left(ad-bc\right)-bd\left(ad-bc\right)=0\Leftrightarrow\left(ac-bd\right)\left(ad-bc\right)=0\)
<=>\(\orbr{\begin{cases}ac=bd\\ad=bc\end{cases}\Leftrightarrow\orbr{\begin{cases}\frac{a}{b}=\frac{d}{c}\\\frac{a}{b}=\frac{c}{d}\end{cases}\left(ĐPCM\right)}}\)
^_^
VM
2 tháng 12 2019
a) Ta có: BH ⊥ d (gt); CK ⊥ d (gt)
=> BH // CK (từ vuông góc đến song song).
=> góc HBC + góc BCK = 1800 (vì 2 góc trong cùng phía)
Mà do tam giác ABC vuông
=> góc ABC + góc ACB = 900
Vậy góc HBA + góc KCA = 900
Trong tam giác vuông AKC có:
góc KAC + góc KCA = 900
=> góc HBA = góc KAC (1)
Ta có: góc H = góc K = 900 (2)
AB = AC (GT) (3)
Từ (1), (2), (3) => tam giác ABH = tam giác ACK (cạnh huyền - góc nhọn).
=> AH = CK (2 cạnh tương ứng)
b) Ta có: tam giác ABH = tam giác ACK (cmt).
=> AK=HB (2 cạnh tương ứng)
Mà AH = CK (chứng minh trên)
=> AH + AK = HB + CK
Mà AH + AK = HK.
=> HK = BH + CK (đpcm)
Chúc bạn học tốt!
12 tháng 1
1: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(a=b\cdot k;c=d\cdot k\)
\(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{bk}{b\left(k+1\right)}=\dfrac{k}{k+1}\)
\(\dfrac{c}{c+d}=\dfrac{dk}{dk+d}=\dfrac{dk}{d\left(k+1\right)}=\dfrac{k}{k+1}\)
Do đó: \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
2: \(\dfrac{2a+b}{a-2b}=\dfrac{2\cdot bk+b}{bk-2b}=\dfrac{b\left(2k+1\right)}{b\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
\(\dfrac{2c+d}{c-2d}=\dfrac{2dk+d}{dk-2d}=\dfrac{d\left(2k+1\right)}{d\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
Do đó: \(\dfrac{2a+b}{a-2b}=\dfrac{2c+d}{c-2d}\)
3: \(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}=\dfrac{b\left(k+1\right)}{b\cdot\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
Do đó: \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
4: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5\cdot bk+3b}{5dk+3d}=\dfrac{b\left(5k+3\right)}{d\left(5k+3\right)}=\dfrac{b}{d}\)
\(\dfrac{5a-3b}{5c-3d}=\dfrac{5\cdot bk-3b}{5\cdot dk-3d}=\dfrac{b\left(5k-3\right)}{d\left(5k-3\right)}=\dfrac{b}{d}\)
Do đó: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)
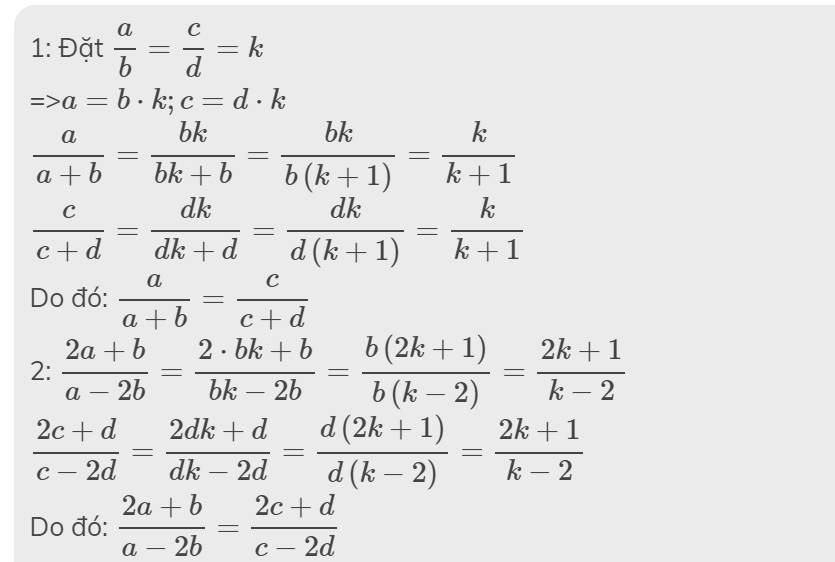
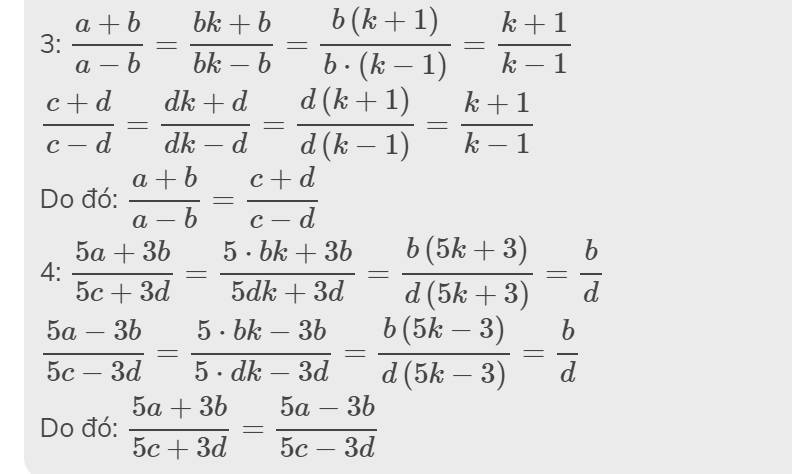
Giải: Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{a+b+c}{b+c+d}\)
hay \(\frac{a}{b}=\frac{a+b+c}{b+c+d}\)
\(\frac{b}{c}=\frac{a+b+c}{b+c+d}\)
\(\frac{c}{d}=\frac{a+b+c}{b+c+d}\)
Nhân vế theo vế của ba đẳng thức trên ta được:
\(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=\left(\frac{a+b+c}{b+c+d}\right)^3\)
mà \(\frac{a}{b}.\frac{b}{c}.\frac{c}{d}=\frac{a}{d}\)
\(\Rightarrow\left(\frac{a+b+c}{b+c+d}\right)^3=\frac{a}{d}\left(đpcm\right)\)
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{a+b+c}{b+c+d}\)
\(\Leftrightarrow\left(\frac{a+b+c}{b+c+d}\right)^3=\frac{a}{b}.\frac{b}{c}.\frac{c}{d}\)
\(\Leftrightarrow\left(\frac{a+b+c}{b+c+d}\right)^3=\frac{a}{d}\)