Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Ảnh ảo, cùng chiều và nhỏ hơn vật.
b)Khỏang cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{9}\)
\(\Rightarrow d'=\dfrac{36}{7}cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{3}{h'}=\dfrac{9}{\dfrac{36}{7}}\Rightarrow h'=\dfrac{12}{7}cm\)

Thấu kính phân kì.
Ta thu được ảnh ảo, cùng chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{12}=\dfrac{1}{18}+\dfrac{1}{d'}\Rightarrow d'=36cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{6}{h'}=\dfrac{18}{36}\Rightarrow h'=12cm\)

Vẽ hình theo tỉ lệ:
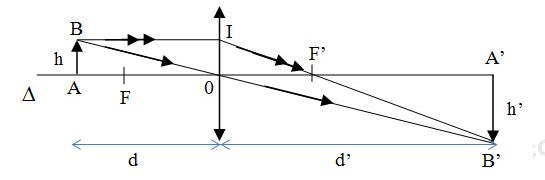
Ảnh A’B’ là ảnh thật, ngược chiều với vật.
- Xét ∆ABO và tam giác ∆A’B’O
Có: góc OAB = góc O'A B' ( đối đỉnh) ; góc A = góc A' = 90 độ
Nên ∆ABO ~ ∆A’B’O
Ta có các tỉ số đồng dạng:
\(\dfrac{AB}{A'B'}=\dfrac{AO}{A'O'}\Leftrightarrow\dfrac{h}{h'}=\dfrac{d}{d'}\)
- Xét ∆OIF’ và ∆F’A’B’
Có:
\(\widehat{IF'O}=\widehat{B'F'A'};\widehat{O}=\widehat{A'}=90^o\)
Nên ∆OIF’ ~ ∆F’A’B’ .
Ta có tỉ số đồng dạng:

Thay số từ đề bài ta có:

Vậy ảnh cách thấu kính 48 cm và A’B’ cao 3 cm.
c)
Từ biểu thức ở phần b ta biến đổi như sau:

Đặt khoảng cách giữa ảnh và vật là:  ; ta được
; ta được

Vì vật tạo ra ảnh thật nên ta có điều kiện là d > 0 và phương trình (*) có nghiệm. Tức là:

Vậy khoảng cách giữa vật và ảnh thật luôn lớn hơn hoặc bằng 4f.
Khoảng cách này ngắn nhất là 4f.
Khi đó giải phương trình (*) ta được d = 2f.

Ảnh A’B’ của AB qua thấu kính là ảnh thật, ngược chiều và lớn bằng vật.
→ Đáp án D