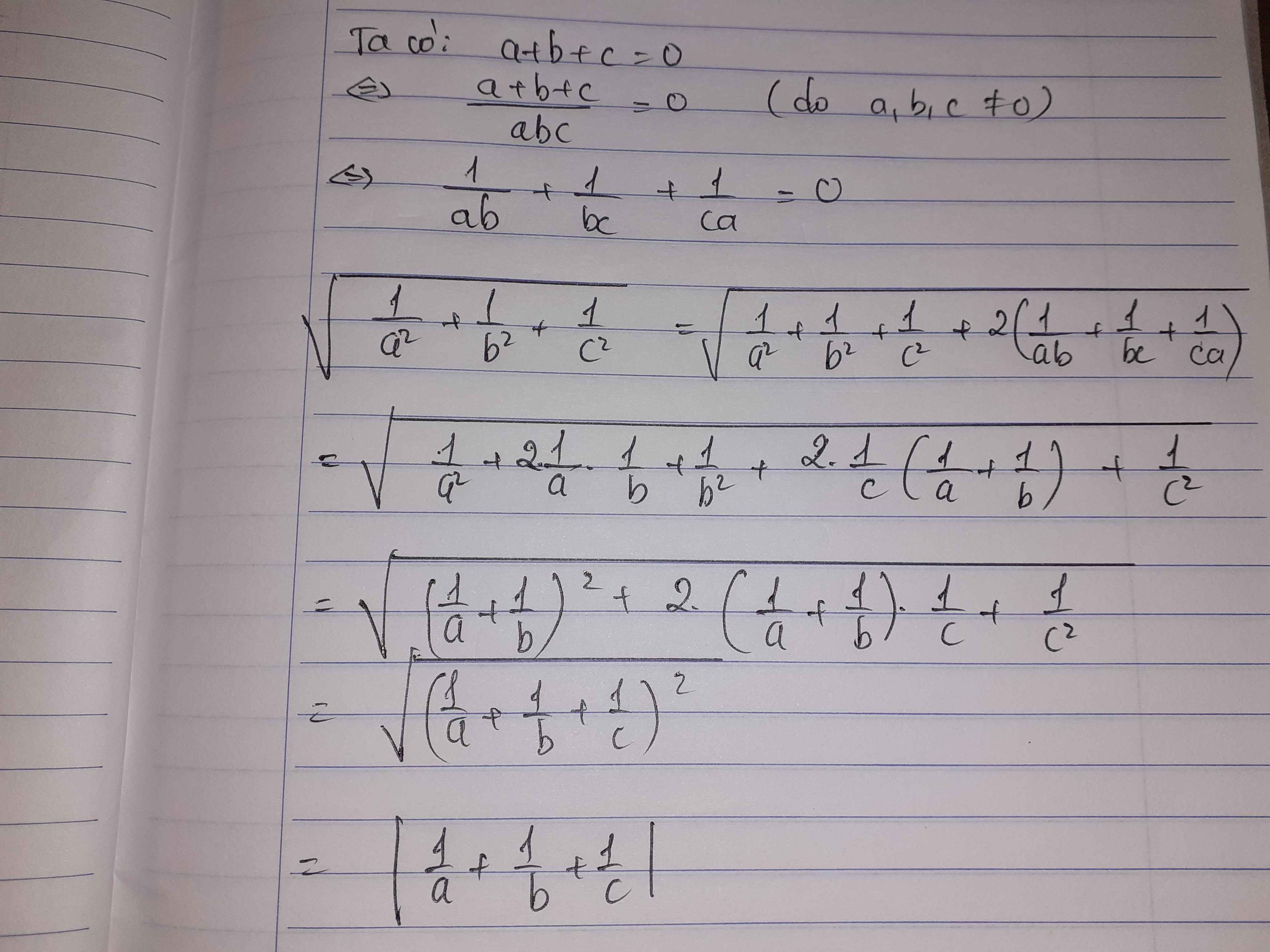Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


$a+b+c \ge \sqrt{ab}+\sqrt{bc}+\sqrt{ca}$
$\Leftrightarrow 2a+2b+2c \ge 2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ca}$
$\Leftrightarrow a-2\sqrt{ab}+b+b-2\sqrt{bc}+c+c-2\sqrt{ca}+a \ge 0$
$\Leftrightarrow (\sqrt{a}-\sqrt{b})^2+(\sqrt{c}-\sqrt{b})^2+(\sqrt{a}-\sqrt{c})^2 \ge 0$ luôn đúng với $a,b,c \ge 0$
Dấu "=" xảy ra khi a=b=c
Ta có: \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
\(\Leftrightarrow2a+2b+2c-2\sqrt{ab}-2\sqrt{bc}-2\sqrt{ca}\ge0\)
\(\Leftrightarrow\left(a-2\sqrt{ab}+b\right)+\left(b-2\sqrt{bc}+c\right)+\left(c-2\sqrt{ca}+a\right)\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2+\left(\sqrt{b}-\sqrt{c}\right)^2+\left(\sqrt{c}-\sqrt{a}\right)^2\ge0\)(luôn đúng với mọi a,b,c không âm)

Đặt \(\left(\sqrt{b^2+c^2};\sqrt{c^2+a^2};\sqrt{a^2+b^2}\right)=\left(x;y;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}a^2=\dfrac{y^2+z^2-x^2}{2}\\b^2=\dfrac{x^2+z^2-y^2}{2}\\c^2=\dfrac{x^2+y^2-z^2}{2}\end{matrix}\right.\)
\(\Rightarrow VT=\dfrac{y^2+z^2-x^2}{2x}+\dfrac{x^2+z^2-y^2}{2y}+\dfrac{x^2+y^2-z^2}{2z}\)
\(VT\ge\dfrac{\left(y+z\right)^2}{4x}+\dfrac{\left(x+z\right)^2}{4y}+\dfrac{\left(x+y\right)^2}{4z}-\dfrac{1}{2}\left(x+y+z\right)\)
\(VT\ge\dfrac{\left(2x+2y+2z\right)^2}{4\left(x+y+z\right)}-\dfrac{1}{2}\left(x+y+z\right)=\dfrac{1}{2}\left(x+y+z\right)\)
\(VT\ge\dfrac{1}{2}\left(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\right)\)
\(VT\ge\dfrac{1}{2}\left(\sqrt{\dfrac{1}{2}\left(a+b\right)^2}+\sqrt{\dfrac{1}{2}\left(b+c\right)^2}+\sqrt{\dfrac{1}{2}\left(c+a\right)^2}\right)\)
\(VT\ge\dfrac{a+b+c}{\sqrt{2}}\) (đpcm)

Để A là số nguyên thì \(3\sqrt{x}+8⋮\sqrt{x}+2\)
=>\(3\sqrt{x}+6+2⋮\sqrt{x}+2\)
=>\(2⋮\sqrt{x}+2\)
mà \(\sqrt{x}+2>2\forall x>0\)
nên A không thể là số nguyên

Ta có: \(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\left(\dfrac{c}{abc}+\dfrac{b}{abc}+\dfrac{a}{abc}\right)}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\cdot\dfrac{a+b+c}{abc}}\)
\(=\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)

\(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}=0\) \(\Rightarrow\dfrac{ayz+bxz+cxy}{xyz}=0\) \(\Rightarrow ayz+bxz+cxy=0\) \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\) \(\Rightarrow\left(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}\right)^2=1\) \(\Rightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\left(\dfrac{xy}{ab}+\dfrac{xz}{ac}+\dfrac{yz}{bc}\right)=1\) \(\Rightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\left(\dfrac{cxy+bxz+ayz}{abc}\right)=1\) \(\Rightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\left(\dfrac{0}{abc}\right)=1\) \(\Rightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+0=1\) \(\Rightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1\)