PT
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ES
0
PT
2
14 tháng 2 2016
Ta có : A = ( 1 + 5 ) + ( 52 + 53 ) + .... + ( 52007 + 52008 )
=> A = 1.6 + 52.( 1 + 5 ) + .... + 52007.( 1 + 5 )
=> A = 1.6 + 52.6 + .... + 52007.6
=> A = 6.( 1 + 52 + ... + 52007 )
Vì 6 ⋮ 6 nên A ⋮ 6 ( đpcm )
=> A = ( 5 + 52 + 53 ) + ( 54 + 55 + 56 ) + .... + ( 52006 + 52007 + 52008 )
=> A = 5.( 1 + 5 + 5.5 ) + 54.( 1 + 5 + 5.5 ) + ... + 52006.( 1 + 5 + 5.5 )
=> A = 5.31 + 54.31 + ... +52006.31
=> A = 31.( 5 + 54 + ... + 52006 )
Vì 31 ⋮ 31 nên A ⋮31 ( đpcm )
14 tháng 12 2022
a: \(=\left(1+2\right)+2^2\left(1+2\right)+...+2^{48}\left(1+2\right)\)
\(=3\left(1+2^2+...+2^{48}\right)⋮3\)
b: \(2^0+2^1+2^2+...+2^{101}\)
\(=\left(1+2+2^2\right)+...+2^{99}\left(1+2+2^2\right)\)
\(=7\left(1+...+2^{99}\right)⋮7\)
c: 2A=2+2^2+...+2^101
=>A=2^101-1
PT
1
CM
10 tháng 3 2019
Ta có A = 2A – A = 2( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 ) – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 2 + 4 + 2 3 + 2 4 + . . . + 2 51 – ( 1 + 2 + 2 2 + 2 3 + . . . + 2 50 )
= 6 + 2 3 + 2 4 + . . . + 2 51 – ( 7 + 2 3 + . . . + 2 50 ) = 2 51 - 1
Suy ra : A + 1 = 2 51
Vậy A+1 là một lũy thừa của 2
PT
1
TT
1
AH
Akai Haruma
Giáo viên
30 tháng 11 2021
Lời giải:
$A=(1+2)+(2^2+2^3)+....+(2^{2020}+2^{2021})$
$=3+2^2(1+2)+....+2^{2020}(1+2)$
$=3+3.2^2+....+3.2^{2020}$
$=3(1+2^2+....+2^{2020})\vdots 3$
Ta có đpcm.
BX
3
21 tháng 9 2023
\(A=1+2+2^2+...+2^{2018}\)
\(2A=2+2^3+2^4+...+2^{2019}\)
\(A=2A-A=1-2^{2019}\)
\(B-A=2^{2019}-\left(1-2^{2019}\right)\)
\(B-A=2^{2019}-1+2^{2019}\)
\(B-A=1\)
21 tháng 9 2023
`#3107`
\(A=1+2+2^2+2^3+...+2^{2018}\) và \(B=2^{2019}\)
Ta có:
\(A=1+2+2^2+2^3+...+2^{2018}\)
\(2A=2+2^2+2^3+...+2^{2019}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2019}\right)-\left(1+2+2^2+2^3+...+2^{2018}\right)\)
\(A=2+2^2+2^3+...+2^{2019}-1-2-2^2-2^3-...-2^{2018}\)
\(A=2^{2019}-1\)
Vậy, \(A=2^{2019}-1\)
Ta có:
\(B-A=2^{2019}-2^{2019}+1=1\)
Vậy, `B - A = 1.`
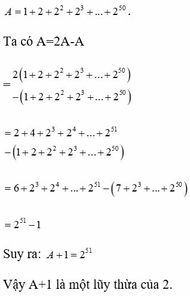
a) Ta có A = 1 + 2 + 22 + 23 + .... + 28 + 29
= (1 + 2) + (22 + 23) + .... + (28 + 29)
= (1 + 2) + 22.(1 + 2) + .... + 28 . (1 + 2)
= 3 + 22 .3 + .... + 28 . 3
= 3.(1 + 22 + .... + 28) \(⋮\)3
Vậy A \(⋮\)3 (đpcm)
b) A = 1 + 2 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29
= (1 + 2 + 22 + 23 + 24) + (25 + 26 + 27 + 28 + 29)
= (1 + 2 + 22 + 23 + 24) + 25.(1 + 2 + 22 + 23 + 24)
= 31 + 25 . 31
= 31.(1 + 25) \(⋮\)31
Vậy A \(⋮\)31 (ĐPCM)
\(a;A=1+2+2^2+...+2^9\)
\(=\left(1+2\right)+2^2\left(1+2\right)+...+2^8\left(1+2\right)\)
\(=\left(1+2\right)\left(1+2^2+...+2^8\right)\)
\(=3\left(1+2^2+...+2^8\right)⋮3\)
\(b;A=\left(1+2+2^2+2^3+2^4\right)+2^5\left(1+2+2^2+2^3+2^4\right)\)
\(=31+2^5\cdot31=31\left(1+2^5\right)⋮31\)