Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp:
Cách giải: Ta có:
x n + 1 = x n 2 ( 2 n + 1 ) x n + 1
⇔ 1 x n + 1 = 2 ( 2 n + 1 ) + 1 x n
Đặt u n = 1 x n
ta có: u n + 1 = 2 ( 2 n + 1 ) + u n
Vậy u 100 = 2 ( 2 . 99 + 1 ) + 2 ( 2 . 98 + 1 ) + . . . 2 ( 2 . 1 + 1 ) + 3 2
⇒ = 39999 2
Vậy x 100 = 39999 2

\(u_n:\left\{{}\begin{matrix}u_1=0;u_1=1\\u_{n+2}=\dfrac{u_{n+1}}{u_{n+1}+u_{n+2}}\end{matrix}\right.\)
Giả sử \(limu_n=a\Rightarrow limu_{n+1}=limu_{n+2}=a\)
\(\Rightarrow a=\dfrac{a}{a+a}=\dfrac{a}{2a}=\dfrac{1}{2}\)
Nên dãy \(u_n\) có giới hạn hữu hạn
vì \(\left\{{}\begin{matrix}u_1=0\\u_2=1>0\end{matrix}\right.\)
\(\Rightarrow u_{n+2}=\dfrac{u_{n+1}}{u_{n+1}+u_{n+2}}>0,\forall n\inℕ\)
\(\Rightarrow a>0\)
\(\Rightarrow limu_n=a=\dfrac{1}{2}\)

Chọn A.
Ta có: 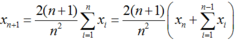
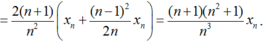
Do đó: 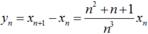
- Ta chứng minh dãy (yn) tăng.
Ta có: 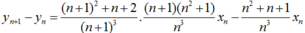
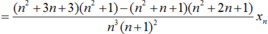
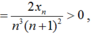
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
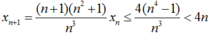
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: 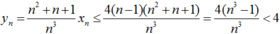
Vậy bài toán được chứng minh.

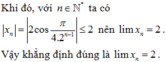
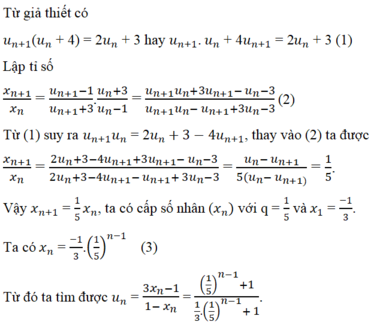

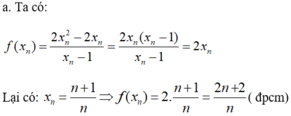
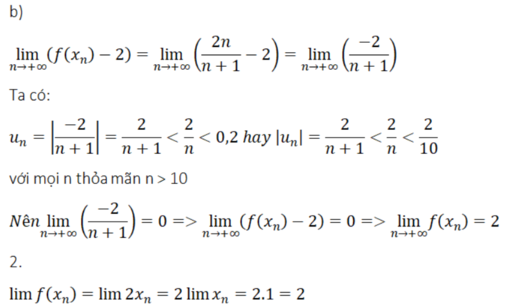
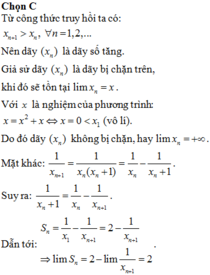
Đề bài sai, dãy tăng và không hề bị chặn trên nên không tồn tại giới hạn