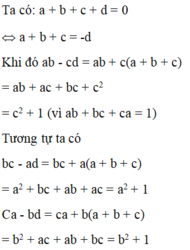Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho a,b,c khác 0 và thỏa mãn ab+bc+ca=0
Hãy tính : \(P=\frac{bc}{a^2}+\frac{ac}{b^2}+\frac{ab}{c^2}\)

\(ab+bc+ca=0\Leftrightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)(vì \(a,b,c\ne0\))
Ta có hằng đẳng thức: \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\)
nên \(x+y+z=0\)thì \(x^3+y^3+z^3=3xyz\)
Từ đó suy ra \(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)
\(\Leftrightarrow\frac{abc}{a^3}+\frac{abc}{b^3}+\frac{abc}{c^3}=3\)
\(\Leftrightarrow P=\frac{bc}{a^2}+\frac{ac}{b^2}+\frac{ab}{c^2}=3\)

\(N=\dfrac{\left(ab\right)^3+\left(bc\right)^3+\left(ca\right)^3}{\left(ab\right)\left(bc\right)\left(ca\right)}\)
Đặt \(\left(ab;bc;ca\right)=\left(x;y;z\right)\Rightarrow x+y+z=0\Rightarrow N=\dfrac{x^3+y^3+z^3}{xyz}\)
\(N=\dfrac{x^3+y^3+z^3-3xyz+3xyz}{xyz}=\dfrac{\dfrac{1}{2}\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]+3xyz}{xyz}=\dfrac{3xyz}{xyz}=3\)

\(\sqrt{a+bc}=\sqrt{a\left(a+b+c\right)+bc}=\sqrt{\left(a+b\right)\left(a+c\right)}\ge\sqrt{\left(a+\sqrt{bc}\right)^2}=a+\sqrt{bc}\)
Tương tự: \(\sqrt{b+ac}\ge b+\sqrt{ac}\) ; \(\sqrt{c+ab}\ge c+\sqrt{ab}\)
\(\Rightarrow VT\ge a+b+c+\sqrt{ab}+\sqrt{bc}+\sqrt{ca}-\sqrt{ab}-\sqrt{bc}-\sqrt{ca}\)
\(\Rightarrow VT\ge a+b+c=1\)
Dấu "=" xảy ra khi \(a=b=c=\frac{1}{3}\)

ta có \(ab+bc+ca=0\)
\(\Rightarrow\frac{ab+bc+ca}{abc}=0\)
\(\Rightarrow\frac{ab}{abc}+\frac{bc}{abc}+\frac{ca}{abc}=0\)
\(\Rightarrow\frac{1}{c}+\frac{1}{a}+\frac{1}{b}=0\)
hay \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)
đặt \(\frac{1}{a}=x;\frac{1}{b}=y;\frac{1}{c}=z\) ta có:
\(x+y+z=0\)
\(\Leftrightarrow x+y=-z\)
\(\Leftrightarrow\left(x+y\right)^3=\left(-z\right)^3\)
\(\Leftrightarrow\left(x+y\right)^3=-z^3\)
ta lại có: \(x^3+y^3+z^3\)
\(=x^3+y^3-\left(x+y\right)^3\)
\(=x^3+y^3-x^3-3xy\left(x+y\right)-y^3\)
\(=-3xy\left(-z\right)\)
\(=3xyz\)
từ đây suy ra \(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)
\(\Leftrightarrow\frac{abc}{a^3}+\frac{abc}{b^3}+\frac{abc}{c^3}=\frac{bc}{a^2}+\frac{ac}{b^2}+\frac{ba}{c^2}=\frac{3abc}{abc}\) \(=3\) ( nhân với abc cho cả 2 vế của biểu thức )
vậy \(N=3\)