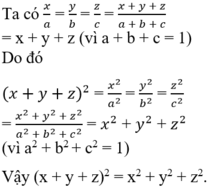Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có: \(a+b+c=1\Leftrightarrow\left(a+b+c\right)^2=1\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}\)
\(\Rightarrow\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}=\dfrac{\left(x+y+z\right)^2}{\left(a+b+c\right)^2}=\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\)
\(\Rightarrow\left(x+y+z\right)^2=x^2+y^2+z^2\) (do \(\left(a+b+c\right)^2=a^2+b^2+c^2=1\))

\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) ⇒ \(\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x^2}{a^2}\) = \(\dfrac{y^2}{b^2}\) = \(\dfrac{z^2}{c^2}\) = \(\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}\) = \(\dfrac{x^2+y^2+z^2}{1}\) = \(x^2+y^2+z^2\) (1)
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}\) = \(\dfrac{x+y+z}{1}\) = \(x+y+z\)
\(\dfrac{x}{a}\) = \(x+y+z\) ⇒ \(\dfrac{x^2}{a^2}\) = (\(x+y+z\))2 (2)
Từ (1) và (2) ta có :
\(\dfrac{x^2}{a^2}\) = \(x^2\) + y2 + z2 = ( \(x+y+z\))2 (đpcm)
⇒
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
= = = = = (1)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
= =
= ⇒ = ()2 (2)
Từ (1) và (2) ta có :
= + y2 + z2 = ( )2 (đpCm)

Áp dụng tính chất các dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}=\dfrac{x+y+z}{1}\)
\(x=a\left(x+y+z\right)=x^2=a^2.\left(x+y+z\right)^2\)
\(y=b\left(x+y+z\right)=y^2=b^2\left(x+y+z\right)^2\)
\(z=c\left(x+y+z\right)=z^2=c^2.\left(x+y+z\right)^2\)
\(\Rightarrow x^2+y^2+z^2=a^2\left(x+y+z\right)^2+b^2\left(x+y+z\right)^2+c^2\left(x+y+z\right)^2\)
\(=\left(x+y+z\right)^2\left(a^2+b^2+c^2\right)=\left(x+y+z\right)^2\) (do \(a^2+b^2+c^2=1\))
https://lazi.vn/edu/exercise/864720/cho-a-b-c-a2-b2-c2-1-va-x-a-y-b-z-c-chung-minh-rang-x-y-z2-x2-y2-z2
liệt phím? Mù mắt?

minh mới giải được phần đầu thui nhe!!!!!!!
Ta có: a+b+c=a^2+b^2+c^2=1
Vì x:y:z=a:b:c nên ta có:
x/a=y/b=z/c
Áp dcụng công thức của dãy tỉ số bằng nhau ta có:
x/a=y/b=z/c=(x+y+z)/(a+b+c)=(x+y+z)/1=x+y+z


Ta có: \(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}\Rightarrow\frac{x^2}{a^2}=\frac{y^2}{b^2}=\frac{z^2}{c^2}\)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=\frac{x+y+z}{a+b+c}=x+y+z\)
\(\Rightarrow\frac{x^2}{a^2}=\frac{y^2}{b^2}=\frac{z^2}{c^2}=\left(x+y+z\right)^2\left(1\right)\)
Lại áp dụng tính chất của dãy tỉ số = nhau có:
\(\frac{x^2}{a^2}=\frac{y^2}{b^2}=\frac{z^2}{c^2}=\frac{x^2+y^2+z^2}{a^2+b^2+c^2}=x^2+y^2+z^2\left(2\right)\)
Từ (1) và (2) => (x + y + z)2 = x2 + y2 + z2 (đpcm)