Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có
log 6 300 = log 6 3 + log 6 100 = log 6 3 + 2 log 6 10 = log 6 3 + 2 log 6 2 + 2 log 6 5 = 1 1 + log 3 2 + 2 1 + log 2 3 + 2 log 5 3 + log 5 2 = 1 1 + 1 a + 2 1 + a + 2 1 b + 1 a b = a a + 1 + 2 1 + a + 2 a b a + 1 = a + 2 a b + 2 1 + a .
Vậy m = 1, n = 2.
Ta có m + n = 3.

Đáp án C
* log 1 16 x xác định khi x > 0
* log 16 log 1 16 x xác định khi log 1 16 x > 0 = log 1 16 1 ⇔ 0 < x < 1
* log 1 4 log 16 log 1 16 x xác định khi
log 16 log 1 16 x > 0 = log 16 1 ⇒ log 1 16 x > 1 = log 1 16 1 16 ⇒ x < 1 16
* log 4 log 1 4 log 16 log 1 16 x xác định khi
log 1 4 log 16 log 1 16 x > 0 = log 1 4 1 ⇒ log 16 log 1 16 x < 1 = log 16 16
⇒ log 1 16 x < 16 = log 1 16 1 16 16 ⇒ x > 1 16 16
* log 1 2 log 4 log 1 4 log 16 log 1 16 x xác định khi
log 4 log 1 4 log 16 log 1 16 x > 0 = log 4 1
⇒ log 1 4 log 16 log 1 16 x > 1 = log 1 4 1 4 ⇒ log 16 log 1 16 x < 1 4 = log 16 2
⇒ log 1 16 x < 2 = log 1 16 1 16 2 ⇒ x > 1 16 2
Kết hợp tất cả các điều kiện ta được
1 16 2 < x < 1 16 ⇒ D = 1 16 2 ; 1 16 ⇒ b − a = 15 256 ⇒ m + n = 271

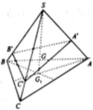
Gọi G 1 là trọng tâm của tam giác ABC. Khi đó
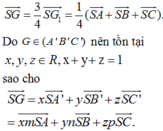
So sánh hai đẳng thức trên ta suy ra
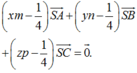
Nhưng do S A → ; S B → ; S C → là ba vecto không đồng phẳng nên đẳng thức trên xảy ra khi và chỉ khi
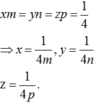
Từ đây và do x + y + z = 1 ta thu được 1 m + 1 n + 1 p = 4
Chọn C.

Đáp án B.
Từ
f x . f ' x = 2 x f 2 x + 1 ⇒ f x . f ' x f 2 x + 1 = 2 x ⇒ ∫ f x . f ' x f 2 x + 1 d x = ∫ 2 x d x
(1)
Đặt
f 2 x + 1 = t ⇒ f 2 x = t 2 − 1 ⇒ 2 f x . f ' x d x = 2 t d t ⇒ f x . f ' x d x = t d t
Suy ra ∫ f x . f ' x f 2 x + 1 x = ∫ t d t t = ∫ d t = t + C 1 = f 2 x + 1 + C 1 và ∫ 2 x d x = x 2 + C 2
Từ (1) ta suy ra f 2 x + 1 + C 1 = x 2 + C 2 . Do f 0 = 0 nên C 2 − C 1 = 1 .
Như vậy
f 2 x + 1 = x 2 + C 2 − C 1 = x 2 + 1 ⇒ f 2 x = x 2 + 1 2 − 1 = x 4 + 2 x 2
⇒ f x = x 4 + 2 x 2 = x x 2 + 2 = x x 2 + 2
(do x ∈ 1 ; 3 ).
Ta có f ' x = x 2 + 2 + x 2 x 2 + 2 = 2 x 2 + 1 x 2 + 2 > 0, ∀ x ∈ ℝ ⇒ Hàm số f x = x x 2 + 2 đồng biến trên R nên f x cũng đồng biến trên 1 ; 3 .
Khi đó M = max 1 ; 3 f x = f 3 = 3 11 và m = min 1 ; 3 f x = f 1 = 3 .
Vậy
P = 2 M − m = 6 11 − 3 ⇒ a = 6 ; b = 1 ; c = 0 ⇒ a + b + c = 7

không có vì nếu a/b=a.m/b.n thì chia 2 vế cho a/b ta được 1=m/n hay m=n (trái giả thiết)
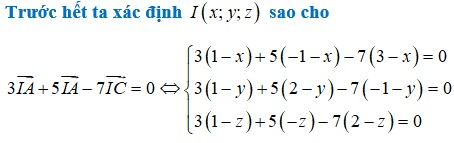
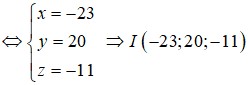

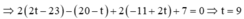
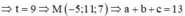


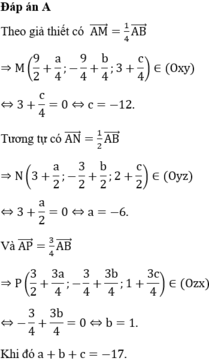
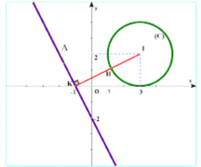

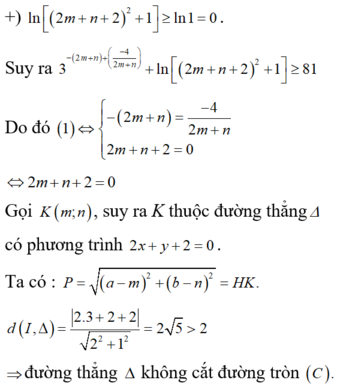

Đáp án D
Ta có: a m . b m = a b m .