
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
$S=3^0+3^2+3^4+...+3^{2002}$
$3^2S=3^2+3^4+3^6+...+3^{2004}$
$3^2S-S=(3^2+3^4+3^6+...+3^{2004})-(3^0+3^2+3^4+...+3^{2002})$
$8S=3^{2004}-3^0=3^{2004}-1$
$S=\frac{3^{2004}-1}{8}$
b.
$S=(3^0+3^2+3^4)+(3^6+3^8+3^{10})+....+(3^{1998}+3^{2000}+3^{2002})$
$=(3^0+3^2+3^4)+3^6(3^0+3^2+3^4)+....+3^{1998}(3^0+3^2+3^4)$
$=(3^0+3^2+3^4)(1+3^6+...+3^{1998})$
$=91(1+3^6+...+3^{1998})=7.13(1+3^6+...+3^{1998})\vdots 7$
Ta có đpcm.

Số hạng thứ 23 của A là:
(23 - 1) x 2 + 30 = 74
Đáp số: 74
Dãy số trên có số các số hạng là :
(96 - 30) :2+1=34( số hạng )
Gọi số thứ 23 là a
Theo đề bài ta có :
(a - 30) : 2+1=23
(a - 30) : 2=23 - 1
(a - 30) : 2 = 22
a - 30 = 22 x 2
a - 30 = 44
a = 44 + 30
a = 74
Học tốt nha em !!!

xét hieeij A - B chưa làm thử đi nó mà dương thì A > B và ngược lại

b: \(S=\left(3^0+3^2+3^4\right)+...+3^{1998}\left(3^0+3^2+3^4\right)\)
\(=91\cdot\left(1+...+3^{1998}\right)⋮7\)

A =30 + 32 +34 +........+ 96 + 98
tìm số hạng thứ 23 của dãy số trên
Bài làm :
số 23 của dãy trên là số 74
học tốt
&YOUTUBER&

b: \(S=3^0+3^2+3^4+...+3^{2002}\)
\(=\left(3^0+3^2+3^4\right)+...+3^{1998}\left(3^0+3^2+3^4\right)\)
\(=91\cdot\left(1+...+3^{1998}\right)⋮7\)


\(A=3+3^2+3^3+...+3^{2012}\\ A=\left(3+3^2+3^3+3^4\right)+...+\left(3^{2009}+3^{2010}+3^{2011}+3^{2012}\right)\\ A=120+...+3^{2008}.120\\ A=120.\left(1+...+3^{2008}\right)⋮120\)

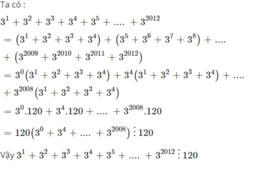
\(3^2a=3^2.\left(3^0+3^2+...+3^{100}\right)\)
\(3^2a=3^2+3^4+3^6+...+3^{102}\)
\(3^2a-a=\left(3^2+3^4+...+3^{102}\right)-\left(3^0+3^2+3^4+...+3^{100}\right)\)
\(8a=3^{102}-1\)
\(a=\frac{3^{102}-1}{8}\)
thank you cool queen