
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A)(0;0)(1;1)
B)Với n = 1 thì 1! = 1 = 1² là số chính phương .
Với n = 2 thì 1! + 2! = 3 không là số chính phương
Với n = 3 thì 1! + 2! + 3! = 1+1.2+1.2.3 = 9 = 3² là số chính phương
Với n ≥ 4 ta có 1! + 2! + 3! + 4! = 1+1.2+1.2.3+1.2.3.4 = 33 còn 5!; 6!; …; n! đều tận cùng bởi 0 do đó 1! + 2! + 3! + … + n! có tận cùng bởi chữ số 3 nên nó không phải là số chính phương .
Vậy có 2 số tự nhiên n thỏa mãn đề bài là n = 1; n = 3.
a)xy=x+y
=>xy-x-y=0
=>x(y-1)-(y-1)-1=0
=>x(y-1)-(y-1)=1
=>(y-1)(x-1)=1
=>y-1 và x-1 E Ư(1)={+-1}=>y=2 thì x=2 và y=0 thì x=0
b)Câu này khó quá nhưng ủng hộ nha


3/ => a(b-2) thuộc Ư(3) = {1;3;-1;-3}
Mà a > 0
=> a thuộc {1;3}
Ta có bảng kết quả:
| a | 1 | 3 |
|---|---|---|
| b-2 | 3 | 1 |
| b | 5 | 3 |

Để A nguyên => n + 3 \(⋮\) n + 2 => ( n + 2 ) + 1 \(⋮\) n + 2 Mà : n + 2 \(⋮\) n + 2 => 1 \(⋮\) n + 2 => n + 2 \(\in\) Ư(1) = 1 Ta có : n + 2 = 1 n = - 1 Vậy n = -1 thì A nguyên
Ta có: n+3/n+2 = n+2+1/n+2 = n+2/n+2 +1/n+2 Mà n+2/n+2 là số nguyên => 1/n+2 là số nguyên
Hay n+2 thuộc Ư(1)={1,-1}
Ta có bảng sau
| n+2 | -1 | 1 |
| n | -3 | -1 |
Vậy n thuộc {-3,-1}

để A là số nguyên thì 6n + 42 phải chia hết cho 6n
ta có: 6n + 42 chia hết cho 6n
mà 6n đã chia hết cho 6n nên 42 phải chia hết cho 6n.
vậy ta xét bảng giá trị:
| 6n | n |
| 1 | loại |
| 42 | 7 |
| 2 | loại |
| 21 | loại |
| 6 | 1 |
| 7 | loại |
| 3 | loại |
| 14 | loại |
| -1 | loại |
| -42 | -7 |
| -2 | loại |
| -21 | loại |
| -6 | -1 |
| -7 | loại |
| -3 | loại |
| -14 | loại |
VẬY n = 7;1;-7;-1
MỆT QUÁ

\(A=\frac{6n+42}{6n}=\frac{6n}{6n}+\frac{42}{6n}=1+\frac{7}{n}\)
Để \(A\in Z\)=> \(\Rightarrow7\) chia hết cho \(n\) \(\Rightarrow n\inƯ\left(7\right)=\left\{-1;1;-7;7\right\}\)

Để A là số nguyên thì n+3 chia hết cho n+2
=>n+2+1 chia hết cho n+2
=>\(n+2\in\left\{1;-1\right\}\)
=>\(n\in\left\{-1;-3\right\}\)
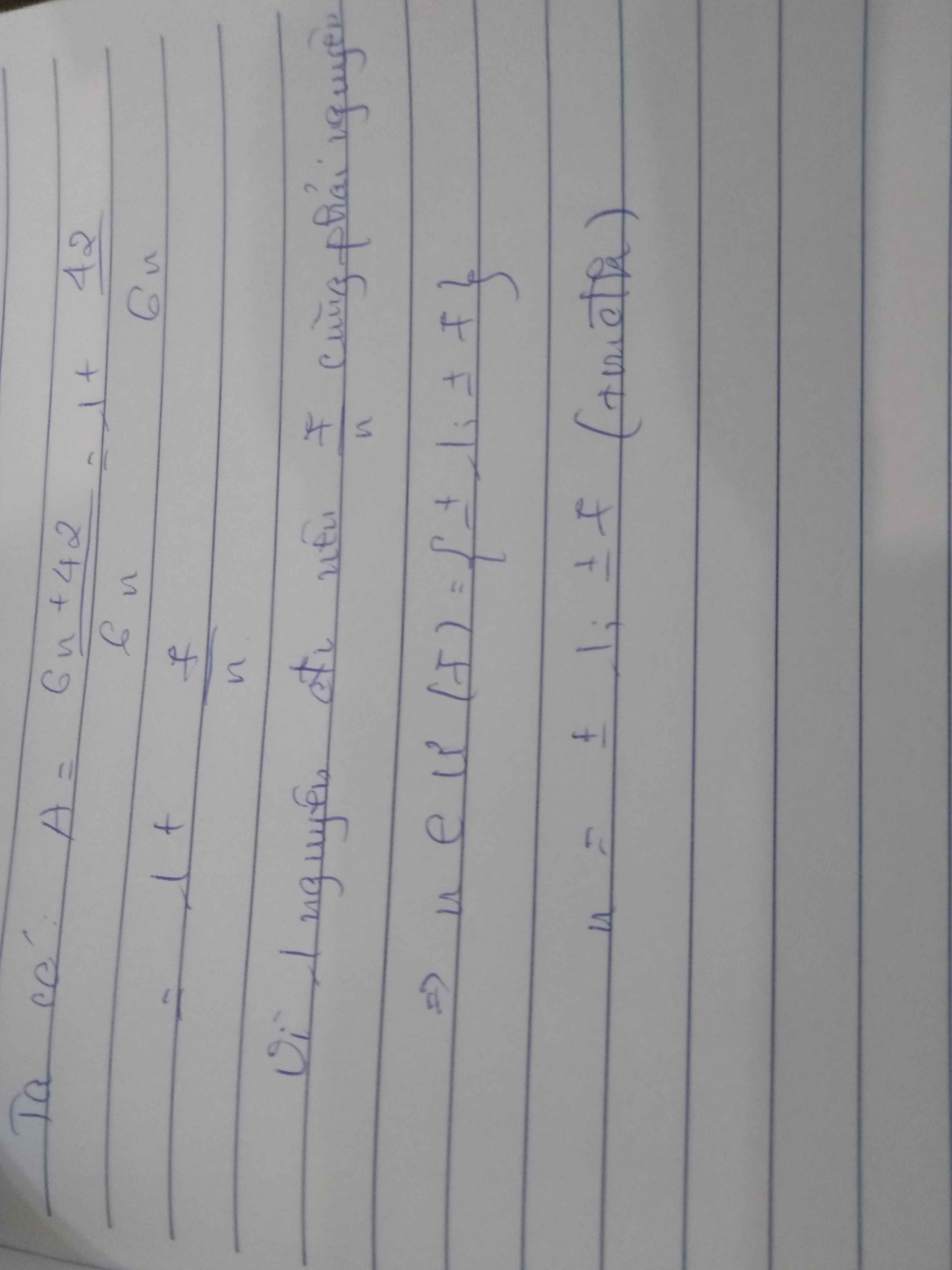
A = 3/n + 2 mà A là một số nguyên, 2 là một số nguyên => 3/n là một số nguyên => 3 ⋮ n => n ∊ Ư(3) = {-3;-1;1;3}. Vậy n ∊ {-3;-1;1;3}