XS
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PN
0
PN
1
21 tháng 11 2021
\(=5+\left(5^2+5^3\right)+\left(5^4+5^5\right)+...+\left(5^{2020}+5^{2021}\right)\\ =5+5\left(5+5^2\right)+5^3\left(5+5^2\right)+...+5^{2019}\left(5+5^2\right)\\ =5+\left(5+5^2\right)\left(5+5^3+...+5^{2019}\right)\\ =5+31\left(5+5^3+...+5^{2019}\right)\)
Vậy BT chia 31 dư 5
AH
Akai Haruma
Giáo viên
13 tháng 12 2022
Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
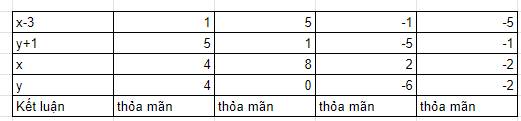
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.
DL
5 tháng 8 2017
a) 235 chia hết cho 5 nên có số dư là 0
476 là số chẵn nên chia hết cho 2,vì có tận cùng là 6 nên chia 5 sẽ dư : 6 - 5 = 1
531 chia cho cả 2 và 5 đều dư 1
987 chia 2 dư 1 chia 5 sẽ dư : 7 - 5 = 2
4309 chia 2 dư 1 chia 5 sẽ dư : 9 - 5 = 4
b) 6314 là số chẵn nên chia hết cho 2, tận cùng là 4 nên chia 5 sẽ dư 4
Tương tự với 3 số còn lại
5 tháng 8 2017
a) 235 chia cho 2: Ta có: 5 : 2 = 2 ( dư 1 ) => 235 chia 2 dư 1
235 chia 5: 5 : 5 = 1. => 235 : 5 dư 0
476 chia 2: Ta có: 6 : 2 = 3. => 476 : 2 dư 0
476 chia 5: Ta có: 6 : 5 = 1 ( dư 1 ) => 476 : 5 dư 1
531 chia 2: Ta có: 11 : 2 = 5 ( dư 1 ) => 531 : 2 dư 1
531 chia 5: Ta có: 11 : 5 = 2 ( dư 1 ) => 531 : 5 dư 1
987 chia 2: Ta có: 7 : 2 = 3 ( dư 1 ) => 987 : 2 dư 1
987 chia 5: Ta có: 7 : 5 = 1 ( dư 2 ) => 987 : 5 dư 2
4309 chia 2: Ta có: 9 : 2 = 4 ( dư 1 ) => 4309 : 2 dư 1
4309 chia 5: Ta có: 9 : 5 = 1 ( dư 4 ) => 4309 : 5 dư 4
MH
28 tháng 12 2021
\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)
\(=4.\left(3+3^3+...+3^{2009}\right)\)
⇒ \(B\) ⋮ 4
29 tháng 12 2021
b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)
19 tháng 12 2021
Biết số chia là 35, thương là 125 và số dư là 5. Ta có số bị chia là
S
24 tháng 7 2016
A = 2 + 22 + 23 +....+ 299
= (2 + 22 + 23) + .... + (297 + 298 + 299)
= 2.(1 + 2 + 4) + .... + 297.(1 + 2 + 4)
= 2.7 + ..... + 297.7
= 7.(2 + .... + 297) chia hết cho 7
DN
24 tháng 7 2016
A=2+22+23+...+299
A=2(1+2+4)+23(1+2+4)+25(1+2+4)+...+297(1+2+4)
A=2.7+23.7+25.7+...+297.7
A=7(2+23+25+27+...+297)
nên biều thức trên chia hết cho 7
A=2+22+23+...+299
A=2(1+2+4+8+16)+25(1+2+4+8+16)+....+295(1+2+4+8+16)
A=2.31+25.31+...+295.31
A=31(2+25+...+295)
vậy A chia hết cho 31 nên số dư của 31 chia A là 0
VH
1
10 tháng 12 2019
A = 50 + 51 + 52 + 53 +...+5100 ( cs 101 so)
A = 50 +51 +( 52 + 53 + 54 )+( 55+56+57)+...+( 598 + 599 + 5100 )
A = 6+ 52.31 +55.31+...+598.31 chia 31 du 6
:)
\(A=\left(1+5+5^2\right)+\left(5^3+5^4+5^5\right)+.....+\left(5^{30}+5^{31}+5^{32}\right)\)
\(A=31.1+31.5^3+......+31.5^{30}\)
\(A=31.\left(1+5^3+......+5^{30}\right)\)\
Vậy A chia hết cho 31 hay chia 31 dư 0