Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ hình
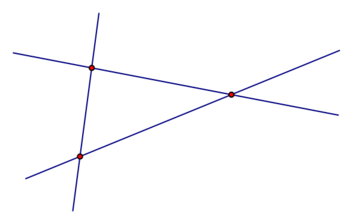
b) Từng cặp đường thẳng cắt nhau tạo ra 3 giao điểm.

Áp dụng công thức tìm số đường thẳng phân biệt khi biết số giao điểm, gọi số giao điểm là n, ta có:
Số đường thẳng phân biệt tạo được\(=1+...+\left(n-1\right)\)
Vậy từ bài toán ta được: \(1+2+...+\left(n-1\right)=8\)
\(\Rightarrow\left[1+\left(n-1\right)\right]\cdot\frac{\left(n-1\right)}{2}=8\)
\(\Rightarrow\left(1+n-1\right)\left(n-1\right):2=8\)
\(\Rightarrow n\cdot\left(n-1\right):2=8\)
\(\Rightarrow n\cdot\left(n-1\right)=16\)

Số giao điểm tất cả là:
\(C^2_{100}\left(giao\right)\)

Ta có công thức: Số giao điểm = [n(n-1)]/2 với n là số đường thẳng đã cho
=> [n(n-1)]/2 = 16
=> n(n-1) = 32
=> n thuộc rỗng
Vậy n thuộc rỗng
Số giao điểm tạo thành là: 5 . ( 5 − 1 ) 2 = 10 giao điểm.